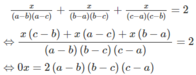
Do a, b, c đôi một khác nhau nên 2(a - b)(b - c)(c - a) ≠ 0. Vậy phương trình đã cho vô nghiệm.
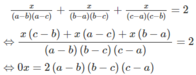
Do a, b, c đôi một khác nhau nên 2(a - b)(b - c)(c - a) ≠ 0. Vậy phương trình đã cho vô nghiệm.
Cho ba số a,b và c đôi một phân biệt.Giai phương trình.
\(\frac{x}{\left(a-b\right)\left(a-c\right)}+\frac{x}{\left(b-a\right)\left(b-c\right)}\frac{x}{\left(c-a\right)\left(c-b\right)}=2\)
giải phương trình (x là ẩn số ; a,b,c là hằng số và đôi một khác nhau)
a) 1/(a+b-x) = 1/a +1/b + 1/x
b) (b-c)(1+a)2 / (x+a2) + (c-a)(1+b)2 / (x+b2) + (a-b)(1+c)2 / (x+c2)
CMR:
a) \(\left(a-b\right)\left(b-c\right)\left(c-a\right)⋮2\) với a, b, c nguyên đôi 1 phân biệt
b) trong 5 số nguyên bất kì phân biệt tồn tại tổng 3 số chia hết cho 3
c) \(\left(x-y\right)^5+\left(y-z\right)^5+\left(z-x\right)^5⋮5\left(x-y\right)\left(y-z\right)\left(z-x\right)\) với x, y, z nguyên đôi 1 phân biệt
Cho số a và ba số b, c, d khác a và thỏa mãn điều kiện c + d = 2b. Giải phương trình
x/(a-b)(a-c) - 2x/(a-b)(a-d) + 3x/(a-c)(a-d) = 4a/(a-c)(a-d)
1/Giải phương trình sau :
\(x-a^2x-\frac{b^2}{b^2-x^2}+a=\frac{x^2}{x^2-b^2}\)
2/ Cho a, b, c là các số khác 0 và đôi một khác nhau , thỏa mãn đẳng thức a + b + c = 0 . Chứng minh rằng :
\(a^3+b^3+c^3+a^2b+ab^2+b^2c+bc^2+c^2a+ca^2=0\)
Giải phương trình \(\frac{\left(x-a\right)\left(x-c\right)}{\left(b-a\right)\left(b-c\right)}+\frac{\left(x-b\right)\left(x-c\right)}{\left(a-b\right)\left(a-c\right)}=1\) ( a,b,c là hằng và khác nhau đôi một)
1/Tìm GTNN của biểu thức:
A=(x+y+1)^2/(xy+x+y) + (xy+x+y)/(x+y+1)^2 ( với x,y là các số thực dương)
2/ cho 3 số thực đôi một phân biệt a,b,c. Chứng minh
a^2/(b-c)^2 + b^2/(c-a)^2 + c^2/(a-b)^2
Cho các số thực \(a,b,c\) đôi một phân biệt sao cho:
\(\hept{\begin{cases}x=\frac{b}{a-b}\\y=\frac{c}{b-c}\\z=\frac{a}{c-a}\end{cases}}\)
Chứng minh rằng giá trị của biểu thức \(xy+yz+zx+x+y+z\)không phụ thuộc vào \(a,b,c\)
cho a, b, c là ba số đôi khác nhau. Cm rằng ít nhất một trong ba số sau đây là số dương:
x=(a+b+c)2-9ab;
y=(a+b+c)2-9bc;
z=(a+b+c)2-9ca