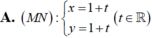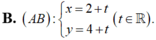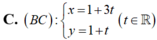Ta có: M N → ( − 6 ; − 6 ) ; M P → ( 3 ; 3 )
Suy ra: M N → = − 2 M P →
Hai vectơ M N → ; M P → ngược hướng nên M nằm giữa N và P .
Đáp án A
Ta có: M N → ( − 6 ; − 6 ) ; M P → ( 3 ; 3 )
Suy ra: M N → = − 2 M P →
Hai vectơ M N → ; M P → ngược hướng nên M nằm giữa N và P .
Đáp án A
Cho ba điểm M, N, P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P. Khi đó các cặp vectơ nào sau đây cùng hướng?
A. M N → v à P N →
B. M N → v à M P →
C. M P → v à P N →
D. N M → v à N P →
Cho đoạn thẳng AB và điểm M nằm giữa hai điểm A và B. khẳng định nào sau đây là đúng?
A. A M → . A B → = − A M . A B
B. A M → . A B → = A M . A B
C. A M → . A B → < 0
D. A M → . A B → > A M . A B
Cho đoạn thẳng AB và điểm M nằm giữa hai điểm A và B. khẳng định nào sau đây là đúng?
A. M A → . M B → > 0
B. M A → . M B → < − M A . M B
C. M A → . M B → = − M A . M B
D. M A → . M B → = M A . M B
Cho điểm B nằm giữa hai điểm A và C, AB = 2a, AC = 6a. khẳng định nào sau đây là đúng?
A. B C → = 4 A C →
B. B C → = A B →
C. B C → = - 2 A B →
D. B C → = - 2 B A →
cho tam giác ABC không là tam giác cân cân. Đường tròn (O) đi qua B, C lần lượt cắt các đoạn thẳng BA, CA tại E, F. Đường tròn ngoại tiếp tam giác ABE cắt đường thẳng CF tại M, N sao cho M nằm giữa C và F. Đường tròn ngoại tiếp tam giác ACF cắt đường thẳng BE tại P, Q sao cho P nằm giữa B và E.Đường thẳng qua N và vuông góc với AN cắt BE tại R. Đường thẳng qua Q và vuông góc với AQ cắt CF tại S. SP giao NR tại U. RM giao QS tại V. Chứng minh rằng NQ, UV, RS đồng quy
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C. BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
1) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Cho hình thang ABCD (AD song song với BC, AD < BC). Các điểm E, F lần lượt thuộc các cạnh AB, CD. Đường tròn ngoại tiếp tam giác AEF cắt đường thẳng AD tại M (M không trùng với A và D, D nằm giữa A và M), đường tròn ngoại tiếp tam giác CEF cắt đường thẳng BC tại điểm N (N không trùng với B và C, B nằm giữa C và N). Đường thẳng AB cắt đường thẳng CD tại điểm P, đường thẳng EN cắt đường thẳng FM tại điểm Q. Chứng minh rằng:
a) Tứ giác EFQP nội tiếp đường tròn.
b) PQ song song với BC và tâm đường tròn ngoại tiếp các tam giác PQE, AMF, CEN cùng nằm trên một đường thẳng cố định.
Cho tam giác ABC. M và N lần lượt thuộc hai tia AB và AC (M, N khác A). Khẳng định nào sau đây là đúng?
A. S A M N S A B C = 3 A M A B . A N A C
B. S A M N S A B C = 1 2 A M A B . A N A C
C. S A M N S A B C = 2 A M A B . A N A C
D. S A M N S A B C = A M A B . A N A C
Cho tam giác ABC. Biết M( 1;1) ; N( 5;5) và P(2; 4) lần lượt là trung điểm của BC; CA; AB. Khẳng định nào sau đây sai?