Question

Cho ABC vuông tại A , trung tuyến Am . Trên tia đối của tia MA lấy điểm D sao cho MD = MA a,Tính Góc ABD

b, CM : TG ABD = TG BAC

c,CM : A/M = 1/2 BC

Vẽ hình giúp mik

helpppppppppppppppppppppppppppppppppppppppppp

Answer 1

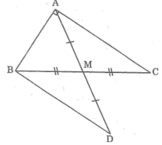
a: Xét ΔMAC và ΔMDB có

MA=MD

\(\hat{AMC}=\hat{DMB}\) (hai góc đối đỉnh)

MC=MB

Do đó; ΔMAC=ΔMDB

=>\(\hat{MAC}=\hat{MDB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//BD

Ta có: AC//BD

AC⊥BA

Do đó; BA⊥BD

=>\(\hat{ABD}=90^0\)

b: ΔMAC=ΔMDB

=>AC=DB

Xét ΔCAB vuông tại A và ΔDBA vuông tại B có

CA=DB

AB chung

Do đó: ΔCAB=ΔDBA

c: ΔCAB=ΔDBA

=>CB=DA

mà \(AM=\frac12AD\)

nên \(AM=\frac12CB\)