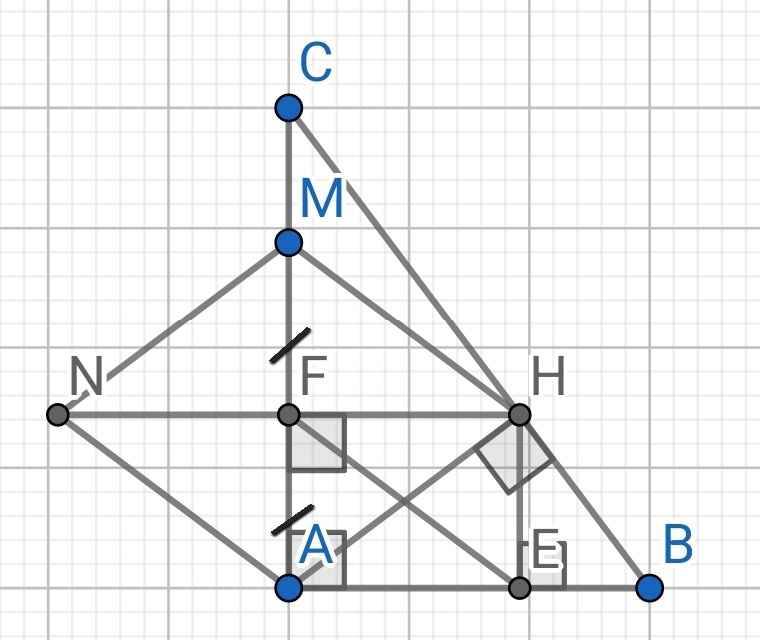
 a) Do HE AB (gt)
a) Do HE AB (gt)
⇒ ∠AEH = 90⁰
Do HF AC (gt)
⇒ ∠AFH = 90⁰
Do ABC vuông tại A (gt)
⇒ ∠FAE = 90⁰
Tứ giác AEHF có:
∠AFH = ∠AEH = ∠FAE = 90⁰
⇒ AEHF là hình chữ nhật
b) Do AEHF là hình chữ nhật (cmt)
⇒ AF // HE và AF = HE
⇒ FM // HE
Do M và A đối xứng nhau qua F
F là trung điểm của AM
⇒ FM = AF
Mà AF = HE (cmt)
⇒ FM = HE
Tứ giác EFMH có:
FM // HE (cmt)
FM = HE (cmt)
⇒ EFMH là hình bình hành
c) Do MN // AH (gt)
⇒ ∠NMF = ∠FAH (so le trong)
Xét hai tam giác vuông: ∆MNF và ∆AHF có:
FM = AF (cmt)
∠NMF = ∠FAH (cmt)
⇒ ∆MNF = ∆AHF (cạnh góc vuông - góc nhọn kề)
⇒ MN = AH (hai cạnh tương ứng)
Tứ giác AHMN có:
MN // AH (gt)
MN = AH (cmt)
⇒ AHMN là hình bình hành
Mà AM ⊥ HN (HF ⊥ AC)
⇒ AHMN là hình thoi













