Các câu hỏi tương tự
A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D.Tia phân giác của góc (BAC) cắt đường tròn ở M,tia phân giác của góc D cắt AM ở I. Chứng minh DI ⊥ AM
Cho đường tròn ( O), Lấy 3 điểm A, B, C thuộc (O ) Sao cho tiếp tuyến A cắt Bỏ tại D .Tia phân giác góc BAC cắt đường tròn ở M, tia phân giác của góc D cắt AM ở I. Chưng minh DI vuông góc AM
Bài 5 : Trên đường tròn (O) lấy ba điểm A, B,C sao cho tiếp tuyến tại A cắt tia BC
Tại D .Tia phân giác của góc BAC cắt đường tròn ở M , tia phân giác của góc D cắt AM ở I . Chứng minh DI vuông góc với AM .
Cho đường tròn (O) dây BC cố định. Điểm A thuộc cung lớn BC. Đường phân giác của góc BAC cắt đường tròn tại D. Các tiếp tuyến của đường tròn O tại C và D cắt nhau tại E. Tia CD cắt AB tại K. Đường thẳng AD cắt CE tại I.
a, CM:BC//DE
b, CM:tứ giác AKIC nội tiếp
c, AD cắt BC tại M. Cm : AB.AC=AM^2+MB.MC
Cho đường tròn (O) dây BC cố định. Điểm A thuộc cung lớn BC. Đường phân giác của góc BAC cắt đường tròn tại D. Các tiếp tuyến của đường tròn O tại C và D cắt nhau tại E. Tia CD cắt AB tại K. Đường thẳng AD cắt CE tại I.
a, CM:BC//DE
b, CM:tứ giác AKIC nội tiếp
c, AD cắt BC tại M. Cm : AB.AC=AM^2+MB.MC
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN2. Cho đường tròn O và O cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O tại D. Tia CB cắt đường tròn O tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF3. Cho tam giác ABC nhọn....
Đọc tiếp
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN = a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN
2. Cho đường tròn O và O' cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O' tại D. Tia CB cắt đường tròn O' tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF
3. Cho tam giác ABC nhọn. Điểm I bất kì trong tam giác. Kẻ IH vuông góc AB , IK vuông góc AC , IL vuông góc AB. Tìm vị trí điểm I sao cho : AL^2 + BH^2 + CK^2 đạt gtnn
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN2. Cho đường tròn O và O cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O tại D. Tia CB cắt đường tròn O tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF3. Cho tam giác ABC nhọn....
Đọc tiếp
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN = a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN
2. Cho đường tròn O và O' cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O' tại D. Tia CB cắt đường tròn O' tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF
3. Cho tam giác ABC nhọn. Điểm I bất kì trong tam giác. Kẻ IH vuông góc AB , IK vuông góc AC , IL vuông góc AB. Tìm vị trí điểm I sao cho : AL^2 + BH^2 + CK^2 đạt gtnn
Cho tam giác ABC nội tiếp đường tròn tâm O và tia phân giác góc A cắt đường tròn tại M, vẽ đường cao AH cắt đường tròn tại N.
a) CM: OA đi qua trung điểm I của tam giác ABC
b) CM: AM là tia phân giác của góc OAH c) Gọi K là điểm đối xứng N qua BC. CM: K là trực tâm của tam giác ABC. d) KI cắt đường tròn tại E. CM: A,O,E thẳng hàng
cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắt dây BC tại Ia/ chứng minh:SA2 SB*SCb/chứng minh:OE⊥BC tại Id/vẽ tiếp tuyến SD của đường tròn (o) D là tiếp điểm D khác A . chứng minh:tứ giác SAOD nội tiếp được đường tròn và I thuộc đường tròn này
Đọc tiếp
cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắt dây BC tại I
a/ chứng minh:SA2 =SB*SC
b/chứng minh:OE⊥BC tại I
d/vẽ tiếp tuyến SD của đường tròn (o) D là tiếp điểm D khác A . chứng minh:tứ giác SAOD nội tiếp được đường tròn và I thuộc đường tròn này




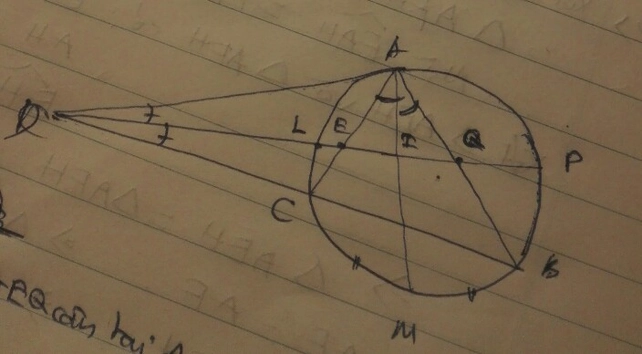
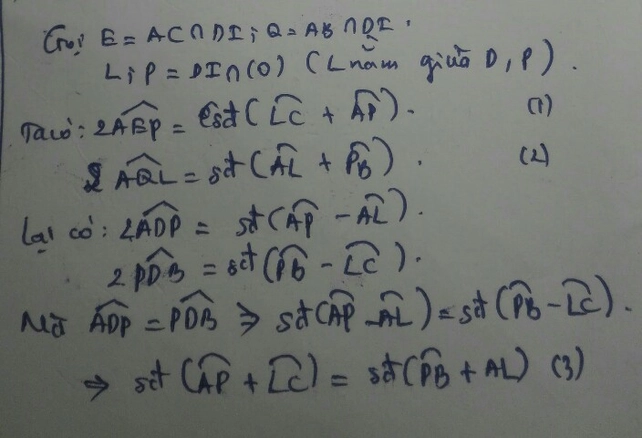
 Bạn tham khảo nhé!
Bạn tham khảo nhé!







