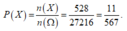Chọn A
Vì là tập tất cả các số tự nhiên có 5 chữ số nên
Số phần tử của không gian mẫu là 
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
có tận cùng bằng 1,do đó 
với 
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng
m
n
p
q
¯
Khi đó: 
- Với m = 1, do 
và q = 3 nên n
≥
4
+) Khi n = 4 thì p > 2 nên p ∈ {4;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi n ≥ 5: Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p ≠ m,n,q nên p có 7 cách chọn. Ta được 35 số thỏa mãn.
- Với m
≥
2 tức là có 7 cách chọn m từ tập {2;4;5;6;7;8;9}. Khi đó 
với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và n
≠
p
≠
m, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
2) M là số có 5 chữ số có dạng m n p q r ¯ Khi đó: m n p q r ¯ ≤ 14285 và r = 3
Do m n p q r ¯ ≤ 14285 nên m chỉ nhận giá trị bằng 1 và n ≤ 4
- Với m=1; n = 0,2 thì p,q là các số tùy ý thuộc tập {0;2;4;5;6;7;8;9} và p ≠ q ≠ n Ta được 2.7.6 = 84 số thỏa mãn.
- Với m=1; n = 4:
+) Khi p = 0 thì q là số tùy ý thuộc tập {2;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;5;6;7;8}. Ta được 5 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 6 + 35 + 392 + 84 + 6 + 5 = 528
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng
.
