Các câu hỏi tương tự
Cho a và b là các số dương. Đơn giản các biểu thức sau:a) b) c) d)
Đọc tiếp
Cho a và b là các số dương. Đơn giản các biểu thức sau:
a) 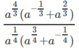
b) 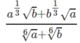
c) 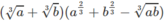
d) 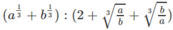
Cho a và b là các số dương. Đơn giản các biểu thức sau:
a
4
3
a
-
1
3
+...
Đọc tiếp
Cho a và b là các số dương. Đơn giản các biểu thức sau: a 4 3 a - 1 3 + a 2 3 a 1 4 a 3 4 + a - 1 4
Cho a, b, x là những số dương. Đơn giản các biểu thức sau:
A
2
a
+
ab
1
2
3...
Đọc tiếp
Cho a, b, x là những số dương. Đơn giản các biểu thức sau: A = 2 a + ab 1 2 3 a - 1 a 3 2 - b 3 2 a - ab 1 2 - a - b a + b
Cho a và b là các số dương. Đơn giản các biểu thức sau:
a
1
3
+
b
1
3
:
2
+
a...
Đọc tiếp
Cho a và b là các số dương. Đơn giản các biểu thức sau: a 1 3 + b 1 3 : 2 + a b 3 + b a 3
Cho hàm số
f
(
x
)
3
x
-
4
+
(
x
+
1
)
.
2
7
-
x
-
6
x
+
3
. Giả sử
m
0
a
b...
Đọc tiếp
Cho hàm số f ( x ) = 3 x - 4 + ( x + 1 ) . 2 7 - x - 6 x + 3 . Giả sử m 0 = a b a , b ∈ ℤ , a b l à p h â n s ố t ố i g i ả n là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 - 4 6 x - 9 x 2 + 2 m - 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. 11
B. 7
C. -1
D. 9
Biết
∫
0
1
x
d
x
5
x
2
+
4
a
b
với a, b là các số nguyên dương và phân thức a/b là tối giản. Tính giá trị của biểu
T
a
2
+
b...
Đọc tiếp
Biết ∫ 0 1 x d x 5 x 2 + 4 = a b với a, b là các số nguyên dương và phân thức a/b là tối giản. Tính giá trị của biểu T = a 2 + b 2
A. T =13
B. T = 26
C. T = 29
D. T = 34
Cho a và b là các số dương. Đơn giản các biểu thức sau:
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho a và b là các số dương. Đơn giản các biểu thức sau: a 1 3 b + b 1 3 a a 6 + b 6
Cho a và b là các số dương. Đơn giản các biểu thức sau:
a
3
+
b
3
a
2
3
+
b...
Đọc tiếp
Cho a và b là các số dương. Đơn giản các biểu thức sau: a 3 + b 3 a 2 3 + b 2 3 - a b 3
Cho a, b, x là những số dương. Đơn giản các biểu thức sau: D = 49 1 - log 7 2 + 5 - log 5 4



