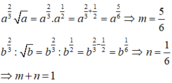Các câu hỏi tương tự
Viết biểu thức
b
a
a
b
3
5
a
,
b
0
về dạng lũy thừa
a
b
m
ta được m ?. A.
2
15
B.
4...
Đọc tiếp
Viết biểu thức b a a b 3 5 a , b > 0 về dạng lũy thừa a b m ta được m = ?.
A. 2 15
B. 4 15
C. 2 5
D. - 2 15
Viết biểu thức
b
a
a
b
3
5
,
a
,
b
0
về dạng lũy thừa
a
b
m
ta được m ?....
Đọc tiếp
Viết biểu thức b a a b 3 5 , a , b > 0 về dạng lũy thừa a b m ta được m = ?.
A. 2 15
B. 4 15
C. 2 5
D. - 2 15
Cho x 0 và y 0. Viết biểu thức
x
4
5
.
x
5
x
6
; về dạng
x
m
và biểu thức
y
4
5
.
y
5
y
6...
Đọc tiếp
Cho x > 0 và y > 0. Viết biểu thức x 4 5 . x 5 x 6 ; về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y n . Ta có m – n = ?
A. -11/6
B. 11/6
C. 8/5
D. -8/5
Cho
x
0
,
y
0
. Viết biểu thức
x
4
5
.
x
5
x
6
về dạng
x
m
và biểu thức
y
4...
Đọc tiếp
Cho x > 0 , y > 0 . Viết biểu thức x 4 5 . x 5 x 6 về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y = y n . Ta có m - n = ?
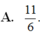
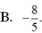
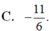
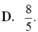
Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-30. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c. A. -3 B. -2 C. 2 D. 3
Đọc tiếp
Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-3=0. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c.
A. -3
B. -2
C. 2
D. 3
Cho x 0; y 0. Viết biểu thức
x
4
5
x
5
x
6
về dạng
x
m
và biểu thức
y
4
5
:
y
5
y...
Đọc tiếp
Cho x > 0; y > 0. Viết biểu thức x 4 5 x 5 x 6 về dạng x m và biểu thức y 4 5 : y 5 y 6 về dạng y n . Ta có x m
A. - 11 6
B. 11 6
C. 8 5
D. - 8 5
Trong không gian Oxyz cho ba điểm A (0;2;-2), B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc mặt phẳng (
α
): 2x -y +2z + 7 0 sao cho biểu thức
3
M
A
→
+
5
M
C
→
-
7
M
C...
Đọc tiếp
Trong không gian Oxyz cho ba điểm A (0;2;-2),
B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc
mặt phẳng ( α ): 2x -y +2z + 7 = 0 sao cho biểu
thức 3 M A → + 5 M C → - 7 M C → đạt giá trị nhỏ nhất.
Tính a+b+c
![]()
![]()
![]()
![]()
a) Tìm hệ thức truy hồi và điều kiện khởi tạo để tính số chuỗi xâu nhị phân độ dài n và không có 3 bít 0 liên tiếp:Đặt Sn là số chuỗi nhị phân độ dài n, không có 3 bit 0 liên tiếp: Một chuỗi dài n (n≥4) thoả mãn điều kiện đầu bài sẽ thuộc một trong các dạng sau: A1 (A là chuỗi có độ dài n - 1, không có 3 bit 0 liên tiếp), gọi số cách là S(n-1) B10 (B là chuỗi có độ dài n - 2, không có 3 bit 0 liên tiếp), gọi số cách là S(n-2) C100 (C là chuỗi có độ dài n - 3, không có 3 bit 0 liên tiếp), gọi số...
Đọc tiếp
a) Tìm hệ thức truy hồi và điều kiện khởi tạo để tính số chuỗi xâu nhị phân độ dài n và không có 3 bít 0 liên tiếp:
Đặt Sn là số chuỗi nhị phân độ dài n, không có 3 bit 0 liên tiếp: Một chuỗi dài n (n≥4) thoả mãn điều kiện đầu bài sẽ thuộc một trong các dạng sau: A1 (A là chuỗi có độ dài n - 1, không có 3 bit 0 liên tiếp), gọi số cách là S(n-1) B10 (B là chuỗi có độ dài n - 2, không có 3 bit 0 liên tiếp), gọi số cách là S(n-2) C100 (C là chuỗi có độ dài n - 3, không có 3 bit 0 liên tiếp), gọi số cách là S(n-3) Nên ta có hệ thức truy hồi: Sn=Sn-1 + Sn-2 + Sn-3 Khởi tạo: S1 = 2, S2 = 4, S3 = 7
b) Giải: ??
giúp mình giải hệ thức ở câu a với ạ!
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng: A.
2
B.
6
C. 6 D. 2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 = 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:
A. 2
B. 6
C. 6
D. 2