Đáp án D
Đặt z 1 = x 1 + y 1 i , x 1 ; y 1 ∈ ℝ . Số phức z 1 được biểu diễn bởi điểm M x 1 ; y 1 .
Đặt z 2 = x 2 + y 2 i , x 2 ; y 2 ∈ ℝ . Số phức z 2 được biểu diễn bởi điểm N x 2 ; y 2 .
Suy ra: z 1 − z 2 = MN .
Em có: z 1 − 5 − i = 3 ⇔ x 1 − 5 + y 1 − 1 i = 3 ⇔ x 1 − 5 2 + y 1 − 1 2 = 9.
Vậy điểm M thuộc đường tròn C : x − 5 2 + y − 1 2 = 9 , có tâm là điểm I(5;1), bán kính R = 3.
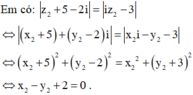
Vậy điểm N thuộc đường thẳng d: x - y +2 = 0.
Dễ thấy đường thẳng d và đường tròn C không cắt nhau.
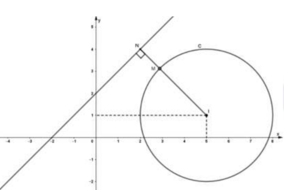
Áp dụng bất đẳng thức tam giác cho bộ ba điểm I, M, N em có:
MN
≥
IM
−
IN
=
IN
−
R
≥
d
I
;
d
−
R
=
5
−
1
+
2
2
−
3
=
−
3
+
3
2
Dấu “=” bằng xảy ra khi và chỉ khi I, M, N thẳng hàng và N là hình chiếu của I trên đường thẳng d.
Vậy z 1 − z 2 min = − 3 + 3 2 .



