\(P=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{x-9}\)
\(=\dfrac{x-\sqrt{x}-6}{x-9}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{x-9}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)
4:
a: P>4/5
=>P-4/5>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{4}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-4\sqrt{x}-12}{5\sqrt{x}+15}>0\)
=>\(\sqrt{x}-2>0\)
=>x>4
b: \(P>\dfrac{2\sqrt{x}}{5}\)
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{2\sqrt{x}}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-2x-6\sqrt{x}}{5\sqrt{x}+15}>0\)
=>\(-2x-\sqrt{x}+10>0\)
=>\(-2x-5\sqrt{x}+4\sqrt{x}+10>0\)
=>\(\left(2\sqrt{x}+5\right)\left(-\sqrt{x}+2\right)>0\)
=>\(-\sqrt{x}+2>0\)
=>0<=x<4
5:
a: \(P-\dfrac{1}{2}=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{1}{2}\)
\(=\dfrac{2\sqrt{x}+4-\sqrt{x}-3}{2\sqrt{x}+6}=\dfrac{\sqrt{x}+1}{2\sqrt{x}+6}>0\)
=>P>1/2
b: \(P-1=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-1=\dfrac{\sqrt{x}+2-\sqrt{x}-3}{\sqrt{x}+3}\)
\(=\dfrac{-1}{\sqrt{x}+3}< 0\)
\(P^2-P=P\left(P-1\right)\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\cdot\dfrac{-1}{\sqrt{x}+3}< 0\)
=>P^2<P
=>P>P^2







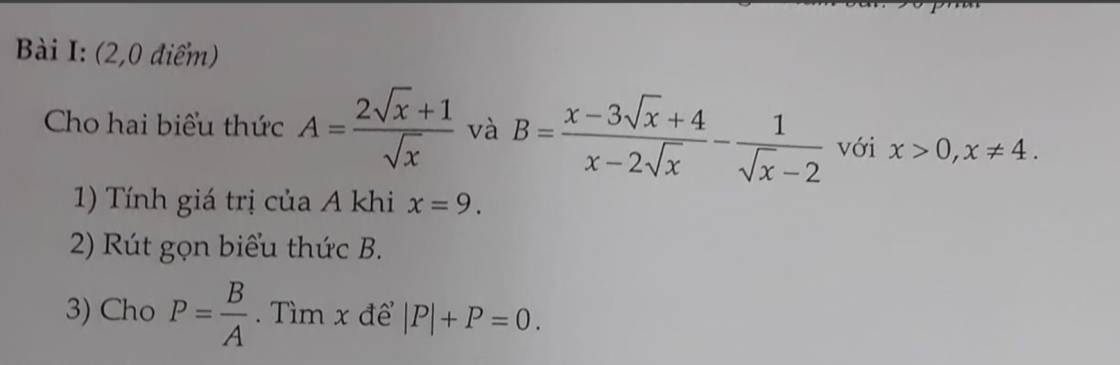


 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần


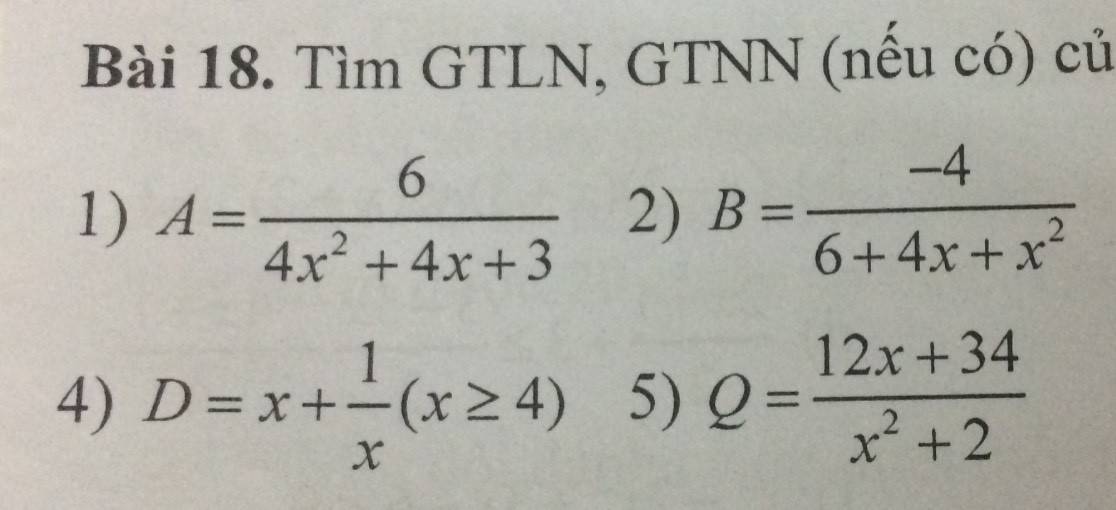


 chỉ cần lm B1 thôi nhé
chỉ cần lm B1 thôi nhé

