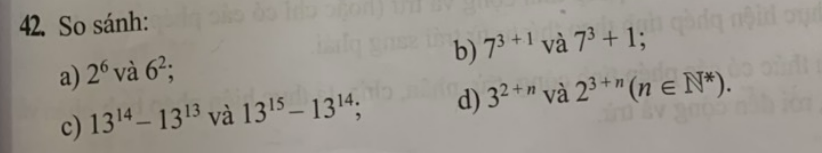c: \(13^{14}-13^{13}=13^{13}\left(13-1\right)=13^{13}\cdot12\)
\(13^{15}-13^{14}=13^{14}\left(13-1\right)=13^{14}\cdot12\)
Do đó: \(13^{14}-13^{13}< 13^{15}-13^{14}\)
d: \(3^{n+2}=3^n\cdot9\)
\(2^{n+3}=2^n\cdot8\)
mà \(3^n>2^n;9>8\)
nên \(3^{n+2}>2^{n+3}\)
cho a+b+c+d khác 0 và a/b+c+d=b/a+c+d=c/a+b+d=d/a+b+c tim gia tri cua A=(a+b/c+d)+(b+c/a+d)+(c+d/a+b)+(d+a/c+d)
cho 2016a+b+c+d/a=a+2016b+c+d/b=a+b+2016c+d/c=a+b+c+2016d/d tính M=a+b/c+d + c+d/d+a + c+d/a+b + d+a/b+c
a/b+c+d=b/a+c+d=c/a+b+d=d/a+b+c Tính P= a+b/c+d+b+c/a+d+c+d/a+b+a+d/b+c
Cho : 2*a+b+c+d/a =a+2*b+c+d/b =a+b+2*c+d/c =a+b+c+2*d/d . Tính M=a+b/c+d -b-c/d+a +c+d/a+d*d+a/b+c .Giúp mình với!
cho biết a +b +c +d khác 0 và a/(b+c+d)=b/(a+c+d)=c/(a+b+d)=d/(a+b+c)
tinh GTBT (a+b)/(c+d)+(b+c)/(a+d)+(c+d)/(a+b)+(d+a)/(b+c)
Cho a, b, c, d thỏa mãn : b+c+d/a=a+c+d/b=a+b+d/c=a+b+c/d
Tính M= a/b+c+d + b/a+c+d + c/a+b+d + d/a+b+c
Cho a+b+c+d khác 0 và a/(b+c+d)=b/(c+d+a)=c/(a+b+d)=d/(a+b+c).
Tính A=(a+c)/(b+d)+(a+c)/(b+d)+(a+c)/(b+d)+(b+c)/(a+d)
Cho a+b+d-2015c/c = a+d+c-2015b/b = a+b+c-2015d/d = b+c+d-2015a/a. Tính F= a+b/c+d + b+c/a+d + a+d/c+b + a+d/c+b + c+d/a+b
Cho: a/b+c+d=b/a+c+d=c/a+b+d=d/a+b+c
TínhA= (a+b/c+d)+(b+c/a+d)+(c+d/a+b)+(d+a/b+c)
cho : a/b+c+d = b/ c+d+a = c/d+a+b = d/a+b+c
tính : M = a+b/c+d = b+c/d+a= c+d/a+b = d+a/b+c
