a: Ta có: \(\hat{A_1}=\hat{B_1}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//HB
b: Ta có: AF//HB
=>\(\hat{F_1}=\hat{B_1}\) (Hai góc so le trong)
=>\(\hat{F_1}=45^0\)
Ta có: \(\hat{F_1}+\hat{F_2}=180^0\) (hai góc kề bù)
=>\(\hat{F_2}=180^0-45^0=135^0\)
c:
Sửa đề: Chứng minh \(\hat{GBA}=90^0\)
Ta có: \(\hat{B_1}+\hat{ABH}=180^0\) (hai góc kề bù)
=>\(\hat{ABH}=180^0-45^0=135^0\)
Vì \(\hat{HBG}<\hat{HBA}\left(45^0<135^0\right)\)
nên tia BG nằm giữa hai tia BH và BA
=>\(\hat{HBG}+\hat{GBA}=\hat{HBA}\)
=>\(\hat{GBA}=135^0-45^0=90^0\)







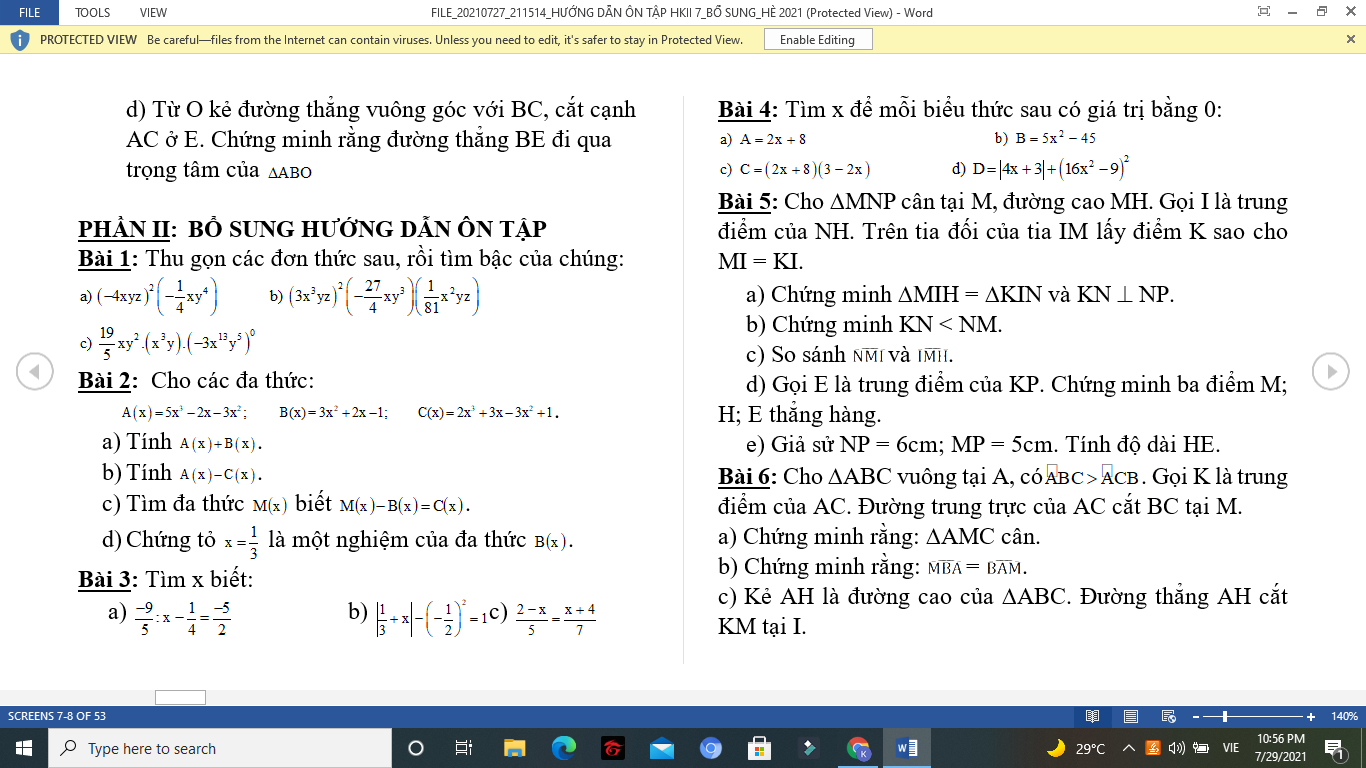

 câu c và câu 13 nhé
câu c và câu 13 nhé