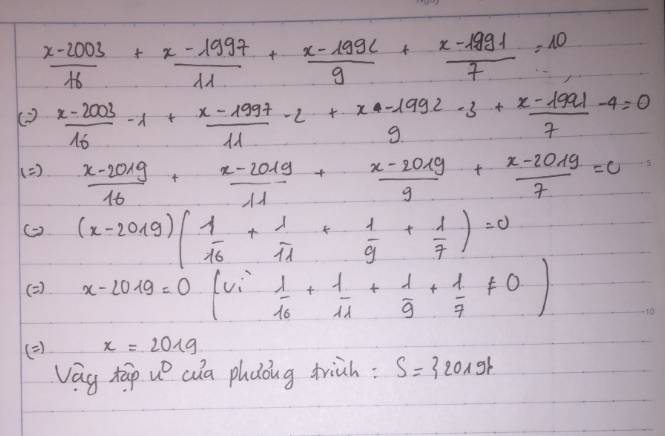`(x-2003)/16 +(x-1997)/11 +(x-1992)/9 +(x-1991)/7=10`
`<=>((x-2003)/16-1)+((x-1997)/11-2)+((x-1992)/9-3)+((x-1991)/7-4)=0`
`<=>(x-2019)/16+ (x-2019)/11 +(x-2019)/9+(x-2019)/7 =0`
`<=> (x-2019)(1/16+1/11+1/9+1/7)=0`
<=> x-2019=0`
`<=> x=2019`
\(\dfrac{x-2003}{16}+\dfrac{x-1997}{11}+\dfrac{x-1992}{9}+\dfrac{x-1991}{7}=10\)
\(\Leftrightarrow\left(\dfrac{x-2003}{16}-1\right)+\left(\dfrac{x-1997}{11}-2\right)+\left(\dfrac{x-1992}{9}-3\right)+\left(\dfrac{x-1991}{7}-4\right)=0\)
\(\Leftrightarrow\left(\dfrac{x-2003}{16}-\dfrac{16}{16}\right)+\left(\dfrac{x-1997}{11}-\dfrac{22}{11}\right)+\left(\dfrac{x-1992}{9}-\dfrac{27}{9}\right)+\left(\dfrac{x-1991}{7}-\dfrac{28}{7}\right)=0\)
\(\Leftrightarrow\dfrac{x-2003-16}{16}+\dfrac{x-1997-22}{11}+\dfrac{x-1992-27}{9}+\dfrac{x-1991-28}{7}=0\)
\(\Leftrightarrow\dfrac{x-2019}{16}+\dfrac{x-2019}{11}+\dfrac{x-2019}{9}+\dfrac{x-2019}{7}=0\)
\(\Leftrightarrow\left(x-2019\right)\left(\dfrac{1}{16}+\dfrac{1}{11}+\dfrac{1}{9}+\dfrac{1}{7}\right)=0\)
\(\Leftrightarrow x-2019=0\) Vì \(\dfrac{1}{16}+\dfrac{1}{11}+\dfrac{1}{9}+\dfrac{1}{7}\ne0\)
\(\Leftrightarrow x=2019\)
Vậy phương trình có 1 nghiệm \(x=2019\)