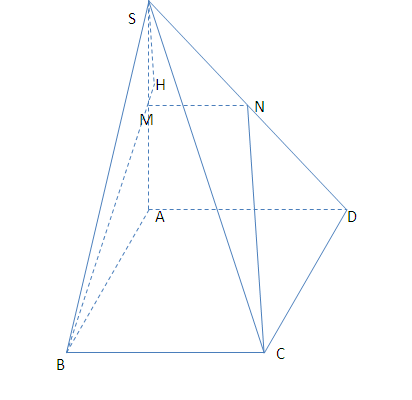
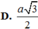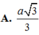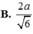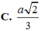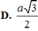Mặt phẳng (BCM) // AD nên nó cắt mặt phẳng (SAD) theo giao tuyến MN//AD
Ta có: BC ⊥ AB và BC ⊥ SA => BC ⊥ BM
Tứ giác BCNM là hình thang vuông BM là đường cao.
có : BC \(\perp\) AB và BC \(\perp\) SA \(\Rightarrow\) BC \(\perp\) BM
Tứ giác BCNM là hình thang vuông BM là đường cao
ta có : SA = AB . tan 60 = \(a\sqrt{3}\)
\(\dfrac{MN}{AD}=\dfrac{SM}{SA}\)
\(\dfrac{MN}{2a}=\dfrac{a\sqrt{3}-\dfrac{a\sqrt{3}}{3}}{a\sqrt{3}}=\dfrac{2}{3}\)
\(\Rightarrow MN=\dfrac{4a}{3}\)
\(BM=\sqrt{a^2+\dfrac{a^2}{3}}\) \(=\dfrac{2a}{\sqrt{3}}\)
diện tích hình thang BCNM là : \(S=\dfrac{2a+\dfrac{4a}{3}}{2}.\dfrac{2a}{\sqrt{3}}=\dfrac{10a^2}{3\sqrt{3}}\)
\(V_{SBCNM}=\dfrac{1}{3}.SH.S_{BCNM}\)
Hạ SH ⊥ BM
ta có : SH \(\perp\) BM
và BC \(\perp\) (SAB) \(\equiv\) (SBM) \(\Rightarrow\) BC \(\perp\) SH . vậy SH \(\perp\) (BMNC)
\(\Rightarrow\) SH là đường cao của khối chóp S.BCNM
trong \(\Delta SBA\) có \(SB=\dfrac{AB}{cos60}=2a\)
\(\Rightarrow\) \(\dfrac{AB}{SB}=\dfrac{AM}{MS}=\dfrac{1}{2}\)
BM là phân giác của góc : \(\left\{{}\begin{matrix}SBH=gt\\SBH=30^o=gt\\SH=SB.sin30^o=2a.\dfrac{1}{2}=a\end{matrix}\right.\)
\(\Leftrightarrow\) thể tích khói chóp S.BCNM là :
\(V=\dfrac{1}{3}.a.\dfrac{10a^2}{3\sqrt{3}}=\dfrac{10\sqrt{3a^2}}{27}\)