Bài 12:
a) Xét ΔOAH vuông tại H và ΔOAK vuông tại K có
OA chung
\(\widehat{HOA}=\widehat{KOA}\)(OA là tia phân giác của \(\widehat{HOK}\))
Do đó: ΔOAH=ΔOAK(cạnh huyền-góc nhọn)
Suy ra: OH=OK(hai cạnh tương ứng)
Bài 12:
b) Ta có: ΔOAH=ΔOAK(cmt)
nên AH=AK(hai cạnh tương ứng)
Ta có: OH=OK(cmt)
nên O nằm trên đường trung trực của HK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AH=AK(cmt)
nên A nằm trên đường trung trực của HK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của HK
hay OA\(\perp\)HK(Đpcm)






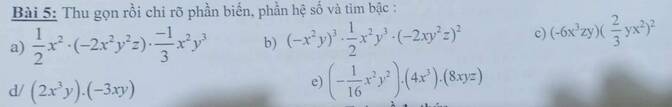








 giúp mình câu 4 mn ơi
giúp mình câu 4 mn ơi


