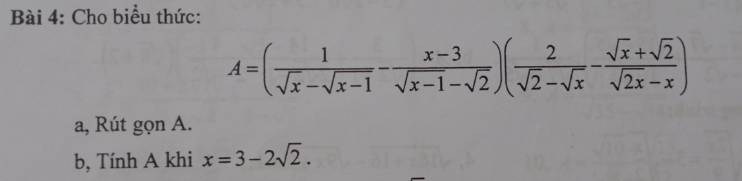\(A=\left(\dfrac{1}{\sqrt{x}-\sqrt{x-1}}-\dfrac{x-3}{\sqrt{x-1}-\sqrt{2}}\right)\left(\dfrac{2}{\sqrt{2}-\sqrt{x}}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{2x}-x}\right)\) (ĐK: \(x\ge1,x\ne2,x\ne3\))
\(A=\left[\dfrac{\sqrt{x}+\sqrt{x-1}}{\left(\sqrt{x}-\sqrt{x-1}\right)\left(\sqrt{x}+\sqrt{x-1}\right)}-\dfrac{\left(x-3\right)\left(\sqrt{x-1}+\sqrt{2}\right)}{\left(\sqrt{x-1}-\sqrt{2}\right)\left(\sqrt{x-1}+\sqrt{2}\right)}\right]\left(\dfrac{2}{\sqrt{2}-\sqrt{x}}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)
\(A=\left[\dfrac{\sqrt{x}+\sqrt{x-1}}{x-x+1}-\dfrac{\left(x-3\right)\left(\sqrt{x-1}+\sqrt{2}\right)}{x-1-2}\right]\left[\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right]\)
\(A=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\)
\(A=\left(\sqrt{x}-\sqrt{2}\right)\cdot-\dfrac{1}{\sqrt{x}}\)
\(A=\dfrac{\sqrt{2}-\sqrt{x}}{\sqrt{x}}\)
b) Ta có: \(x=3-2\sqrt{2}=\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2=\left(\sqrt{2}-1\right)^2\)
Thay vào A ta có:
\(A=\dfrac{\sqrt{2}-\sqrt{\left(\sqrt{2}-1\right)^2}}{\sqrt{\left(\sqrt{2}-1\right)^2}}=\dfrac{\sqrt{2}-\sqrt{2}+1}{\sqrt{2}-1}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)