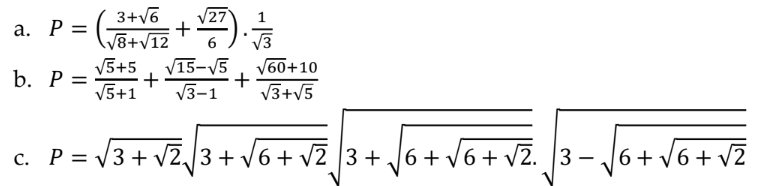Question

cần hỗ trợ gấp

Answer 1

a: \(=\left(\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2}\right)\cdot\dfrac{1}{\sqrt{3}}=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}=1\)

b: \(=\sqrt{5}+\sqrt{5}+2\sqrt{5}=4\sqrt{5}\)

c: \(=\sqrt{3+\sqrt{2}}\cdot\sqrt{3+\sqrt{6+\sqrt{2}}}\sqrt{9-6-\sqrt{6+\sqrt{2}}}\)

\(=\sqrt{3+\sqrt{2}}\cdot\sqrt{3+\sqrt{6+\sqrt{2}}}\cdot\sqrt{3-\sqrt{6+\sqrt{2}}}\)

=căn 3+căn 2*căn 3-căn 2

=căn 9-2=căn 7