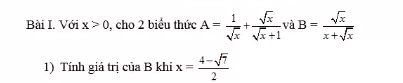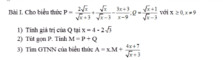a: Xét tứ giác DHEC có \(\widehat{HEC}+\widehat{HDC}=90^0+90^0=180^0\)
nên DHEC là tứ giác nội tiếp
=>D,H,E,C cùng thuộc một đường tròn
b: Xét ΔHBK có
HD là đường cao
HD là đường trung tuyến
Do đó: ΔHBK cân tại H
=>\(\widehat{HBK}=\widehat{HKB}\)
mà \(\widehat{HBK}=\widehat{DAC}\left(=90^0-\widehat{ACB}\right)\)
nên \(\widehat{HKB}=\widehat{DAC}\)
Ta có: \(\widehat{HKB}+\widehat{LKC}=180^0\)(hai góc kề bù)
\(\widehat{DAC}+\widehat{LAH}=180^0\)(hai góc kề bù)
mà \(\widehat{HKB}=\widehat{DAC}\)
nên \(\widehat{LAH}=\widehat{LKC}\)
Xét ΔLAH và ΔLKC có
\(\widehat{LAH}=\widehat{LKC}\)
\(\widehat{ALH}\) chung
Do đó: ΔLAH~ΔLKC
=>\(\dfrac{LA}{LK}=\dfrac{LH}{LC}\)
=>\(LA\cdot LC=LH\cdot LK\)
Gọi X là giao điểm của AO với (O)
=>AX là đường kính của (O)
=>O là trung điểm của XA
Xét ΔABC có
BE,AD là các đường cao
BE cắt AD tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
Xét (O) có
ΔABX nội tiếp
AX là đường kính
Do đó: ΔABX vuông tại B
=>BX\(\perp\)BA
mà CH\(\perp\)BA
nên CH//BX
Xét (O) có
ΔACX nội tiếp
AX là đường kính
Do đó: ΔACX vuông tại C
=>AC\(\perp\)CX
mà BH\(\perp\)AC
nên BH//CX
Xét tứ giác BHCX có
BH//CX
BX//CH
Do đó: BHCX là hình bình hành
=>BC cắt HX tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HX
Xét ΔAHX có
M,O lần lượt là trung điểm của HX,XA
=>MO là đường trung bình của ΔAHX
=>AH=2MO