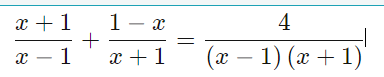f) ... \(\Leftrightarrow x^3+3x^2+3x+1+x^3-3x^2+3x-1=x^2-1+4\)
\(\Leftrightarrow2x^3+6x=x^2-3\) \(\Leftrightarrow\left(2x+1\right)\left(x^2+3\right)=0\) \(\Leftrightarrow2x+1=0\) \(\Leftrightarrow x=-\dfrac{1}{2}\)
g) ... \(\Leftrightarrow x\left(x^2-6x+9\right)=0\) \(\Leftrightarrow x\left(x-3\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
h) ... \(\Leftrightarrow x^2=\dfrac{25}{9}\Leftrightarrow x=\pm\dfrac{5}{3}\)
i) ... \(\Leftrightarrow x^2-4x+4-\left(x^2-x+3x-3\right)=-7\) \(\Leftrightarrow-6x+14=0\) \(\Leftrightarrow x=\dfrac{7}{3}\)
k) ... \(\Leftrightarrow\) 2x - 1 = 0 và x + 5 = 0 => PTVN


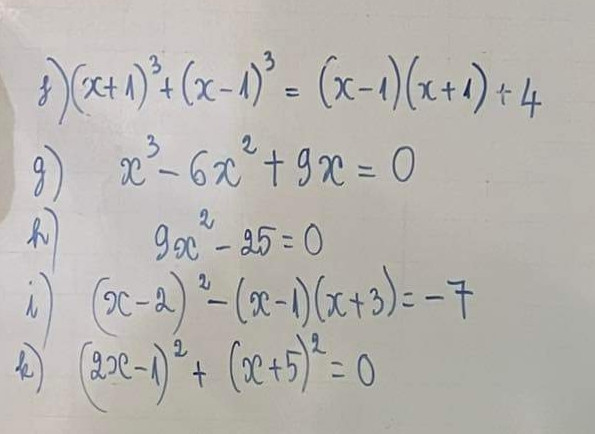 cần gaaps ạ hứa k
cần gaaps ạ hứa k