Chọn D.
Giả sử w = x + yi là một căn bậc hai của số phức z = -3 + 4i.
Ta có:
![]()
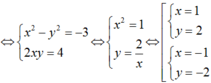
Do đó z có hai căn bậc hai là: z1 = 1 + 2i và z2 = -1 - 2i.
Chọn D.
Giả sử w = x + yi là một căn bậc hai của số phức z = -3 + 4i.
Ta có:
![]()
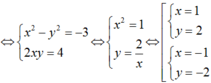
Do đó z có hai căn bậc hai là: z1 = 1 + 2i và z2 = -1 - 2i.
Cho số phức z thay đổi thỏa mãn z - 3 - 4 i ≤ 2 Đặt w = z - 2 2 - 2 i + 1 tập hợp tất cả các điểm biểu diễn số phức w là một hình tròn có diện tích bằng
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính min |w|, với w = z - 2 + 2 i
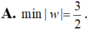
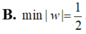
![]()
![]()
Cho số phức z thỏa mãn (1-3i)z+1+i=-z. Môđun của số phức w=13z+2i có giá trị bằng:
A. -2
B. 26 13
C. 10
D. - 4 13
Cho các số phức z, w thỏa mãn |z + 2 - 2i| = |z - 4i|, w=iz+1. Giá trị nhỏ nhất của |w| là:
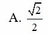
![]()
![]()
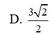
Cho các số phức z, w thỏa mãn z + 2 - 2 i = z - 4 i , w = i z + 1 . Giá trị nhỏ nhất của w là
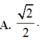
![]()
![]()
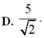
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính m i n w , với w = z - 2 + 2 i .
A. m i n w = 3 2
B. m i n w = 2
C. m i n w = 1
D. m i n w = 1 2
Cho hai số phức z, w thỏa mãn | z - 3 - 2 i | ≤ 1 | w + 1 + 2 i | ≤ | w - 2 - i | . Tìm gía trị nhỏ nhất P m i n của biểu thức P = |z-w|.
A . P m i n = 3 2 - 2 2
B . P m i n = 2 + 1
C . P m i n = 5 2 - 2 2
D . P m i n = 2 2 + 1 2
Cho số phức z = a - 4 i , w = 1 - 2 i . Biết z = 2w, khi đó giá trị của a bằng
A. 1
B. 2
C. -2
D. -4
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Cho số phức z thay đổi, luôn có |z| = 2. Khi đó tập hợp điểm biểu diễn số phức w = (1-2i) z ¯ + 3i là:
A. Đường tròn x 2 + ( y - 3 ) 2 = 2 5
B. Đường tròn x 2 + ( y + 3 ) 2 = 20
C. Đường tròn x 2 + ( y - 3 ) 2 = 20
D. Đường tròn ( x - 3 ) 2 + y 2 = 2 5