Question

Cảm ơn mọi người trước ạ!

Answer 1

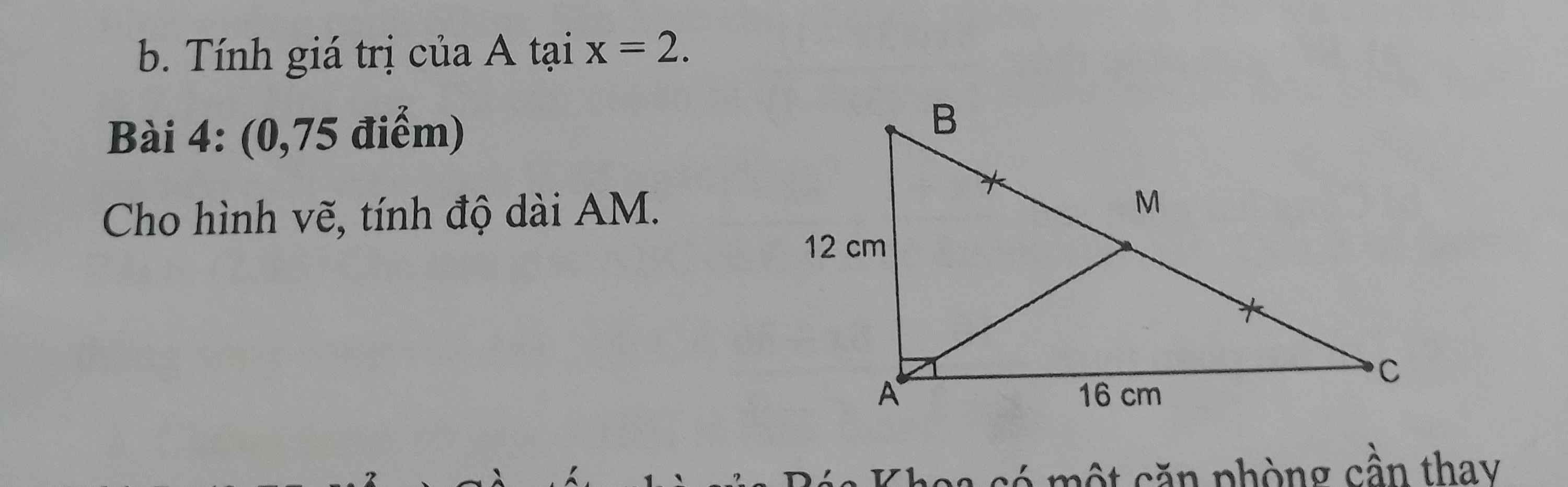
Xét `\triangle ABC` vuông tại `A` có:

    `AB^2+AC^2=BC^2`

`=>12^2+16^2=BC^2 <=>BC=20(cm)`

Có: `AM` là đường trung tuyến của `\trianglw ABC` vuông tại `A`

   `=>AM=1/2BC=1/2 .20=10(cm)`

Answer 2

∆ABC vuông tại A

⇒BC² = AB² + AC² (Pytago)

⇒BC² = 12² + 16² 

= 14+ 256

= 400

⇒BC = 20 (cm)

AM là đường trung tuyến ứng với cạnh huyền BC

⇒AM = BC : 2

= 20 : 2

= 10 (cm)