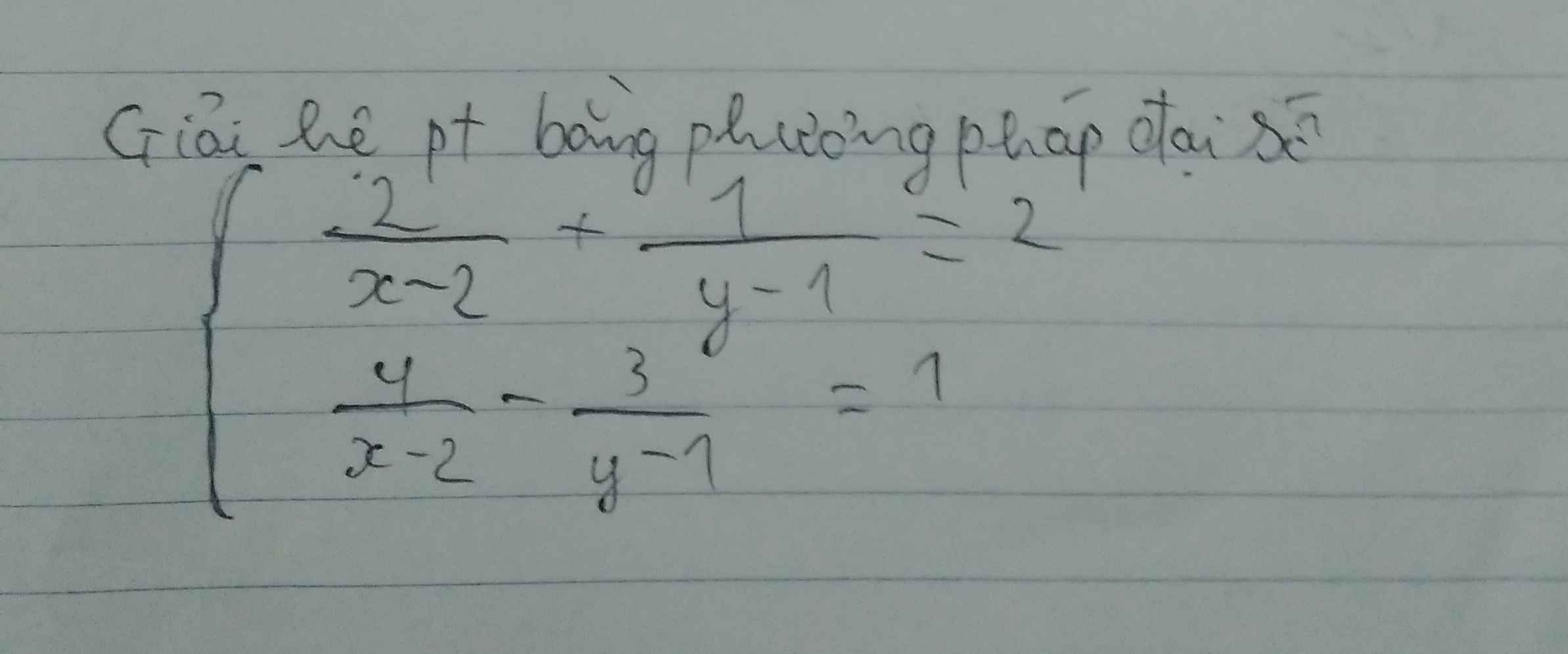ĐKXĐ : \(\left\{{}\begin{matrix}x\ne-3\\y\ne1\end{matrix}\right.\)
- Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+3}=a\\\dfrac{1}{y-1}=b\end{matrix}\right.\)
HPTTT : \(\left\{{}\begin{matrix}a-2b=9\\3a+b=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=9\\6a+2b=12\end{matrix}\right.\)
- Cộng hai phương trình ta được : 7a = 21
=> a = 3
=> b = -3
- Thay lại hệ phương trình ta được ; \(\left\{{}\begin{matrix}\dfrac{1}{x+3}=3\\\dfrac{1}{y-1}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{8}{3}\\y=\dfrac{2}{3}\end{matrix}\right.\) ( TM )
Vậy ..
\(\begin{cases}\dfrac{1}{x+3}-\dfrac{2}{y-1}=9\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{1}{x+3}-\dfrac{2}{y-1}=9\\\dfrac{6}{x+3}+\dfrac{2}{y-1}=12\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{7}{x+3}=21\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{1}{x+3}=3\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}x+3=\dfrac13\\\dfrac{1}{y-1}=6-9=-3\\\end{cases}\)
`<=>` \(\begin{cases}x=\dfrac{-8}{3}\\y=\dfrac23\\\end{cases}\)