Tham khảo
vẽ sơ đồ tư duy hệ thống lại toàn bộ kiến thức hình học lớp 8 - Google Tìm kiếm
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
4 tháng 4 2022 lúc 19:50
Vẽ sơ đồ tư duy về toàn bộ hệ thống kiến thức Hình Học chương III.
giúp mik câu hỏi hóa lớp 8 với khó quá :v
Câu 1
vẽ sơ đồ tư duy hệ thống kiến thức cơ bản sau khi đã học xong bài Bazơ
Câu 2
cũng như Câu 1 nhưng về bài muối
=))))))))))))))
Vẽ sơ đồ tư duy tổng hợp kiến thức về:
-Định nghĩa
-Tính chất
-Dấu hiệu nhận biết
Của các tứ giác sau:
-Hình bình hành
-Hình chữ nhật
-Hình thoi
-Hình vuông.
hãy vẽ sơ đồ tư duy bài nhân đơn thức với đa thức
Vẽ sơ đồ tư duy sơ lược các nội dung chính Hóa 8
Mình bị mất gốc toán hình từ năm lớp 6 -> 8. Vậy liệu có thể học được toán hình lớp 9 hay ko ???
TRẢ LỜI GIÚP MIK VỚI
CÁC BẠN ĐÃ THI LÊN 10 CHO MIK HỎI KIẾN THỨC HÌNH CÓ KHÓ KO??
TRẢ LỜI GIÚP MIK
Vẽ sơ đồ tư duy áp suất ( áp suất rắn + lỏng + khí ) ?
6 tháng 9 2023 lúc 19:05
[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 2) ] |-----------------------------------------------------------------------------|#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị Mất gốc trong môn Toán ở cấp độ THCS(1) Phần số học + Số nguyên tố, phân tích một số ra thừa số nguyên tố - Ở cấp THCS ta cần nắm và hiểu rõ về số nguyên tố Số nguyên tố là số tự nhiên khác 1 và chia hết cho 1 và chia hết cho chính nó VD: 3,5,7,11,13...
Đọc tiếp
[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 2) ]
|-----------------------------------------------------------------------------|
#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS
(1) Phần số học
+ Số nguyên tố, phân tích một số ra thừa số nguyên tố
- Ở cấp THCS ta cần nắm và hiểu rõ về số nguyên tố
Số nguyên tố là số tự nhiên khác 1 và chia hết cho 1 và chia hết cho chính nó
VD: \(3,5,7,11,13,17,19,23,29,...\)
- Cách phân tích 1 số ra thừa số nguyên tố
Bước 1: Nhìn sơ quát số và nhẩm xem số đó chia hết cho 2,3,5 hay 7 không
Bước 2: Xét thương nếu thương không phải số nguyên tố thì tiếp tục phân tích
Bước 3: Tiếp tục phân tích thương dần đến kết quả cuối cùng là 1 số nguyên tố
VD: Phân tích số 35
Ta có: 35 = 7 x 5
+ Ước, bội, ước chung lớn nhất, bội chung nhỏ nhất
- Tập hợp các số mà số đó chia hết được gọi là ước
Được kí hiệu là Ư(x)
- Tập hợp các số chia hết cho số đó được gọi là bội
Được kí hiệu là B(x)
VD: Ư(10)\(=\left\{1;2;5;10\right\}\)
\(B\left(10\right)=\left\{0;10;20;30;40;50;...\right\}\)
- Ước chung là tập hợp ước của số này mà cũng là ước của số kia
Được kí hiệu là: ƯC(x;y)
- Bội chung là tập hợp bội của số này mà cũng là bội của số kia
Được kí hiệu là BC(x;y)
VD: \(Ư\left(12\right)=\left\{1;2;3;4;6;12\right\}\)
\(Ư\left(15\right)=\left\{1;3;5;15\right\}\)
\(\RightarrowƯC\left(12;15\right)=\left\{1;3\right\}\)
\(B\left(9\right)=\left\{0;9;18;27;36;54;...\right\}\)
\(B\left(3\right)=\left\{0;3;6;9;12;15;18;21;24;27;...\right\}\)
\(\Rightarrow BC\left(9;3\right)=\left\{0;9;18;27;..\right\}\)
- Ước chung lớn nhất là ước của số này cũng là ước của số kia nhưng đó là ước chung lớn nhất
Được kí hiệu là: ƯCLN
- Bội nhung nhỏ nhất là bội của số này cũng là bội của số kia nhưng đó là bội chung nhỏ nhất
Được kí hiệu là: BCNN
+ Số hữu tỉ, vô tỉ, số thập phân hữu hạn, vô hạng tuần hoàn, giá trị tuyệt đối
- Số hữu tỉ được biểu diễn dưới dạng \(\dfrac{a}{b}\left(a,b\in Z;b\ne0\right)\)
Tập hợp các số hữu tỉ được kí hiệu là tập hợp Q
- Số thập phân hữu hạn là số hữu tỉ tối giản không có ước nguyên tố khác 2 và 5
VD: \(\dfrac{1}{5};\dfrac{2}{5};\dfrac{5}{2};...\)
- Số thập phân vô hạn tuần hoàn là số hữu tỉ có ước nguyên tố khác 2,5
VD: \(\dfrac{3}{7};\dfrac{1}{6};\dfrac{1}{9};\dfrac{5}{7};...\)
- Cách công trừ nhân chia các số hữu tỉ:
Cộng số hữu tỉ:
\(\dfrac{a}{m}+\dfrac{b}{m}=\dfrac{a+b}{m}\)
Trừ số hữu tỉ:
\(\dfrac{a}{m}-\dfrac{b}{m}=\dfrac{a-b}{m}\)
Nhân số hữu tỉ:
\(\dfrac{a}{n}\cdot\dfrac{b}{m}=\dfrac{a\cdot b}{m\cdot n}\)
Chia số hũu tỉ:
\(\dfrac{a}{n}:\dfrac{b}{m}=\dfrac{a}{n}\cdot\dfrac{m}{b}=\dfrac{a\cdot m}{n\cdot b}\)
- Tính giá trị tuyệt đối của 1 số hữu tỉ:
\(\left\{{}\begin{matrix}khi:x\ge0\Rightarrow\left|x\right|=x\\khi:x< 0\Rightarrow\left|x\right|=-x\end{matrix}\right.\)
VD: \(\left|-5\right|=-\left(-5\right)=5\left(-5< 0\right)\)
\(\left|2\right|=2\left(2>0\right)\)
(2) Phần hình học
+ Một đường thẳng cắt 2 đường thẳng song song, hai góc so le trong, đồng vị, trong cùng phía
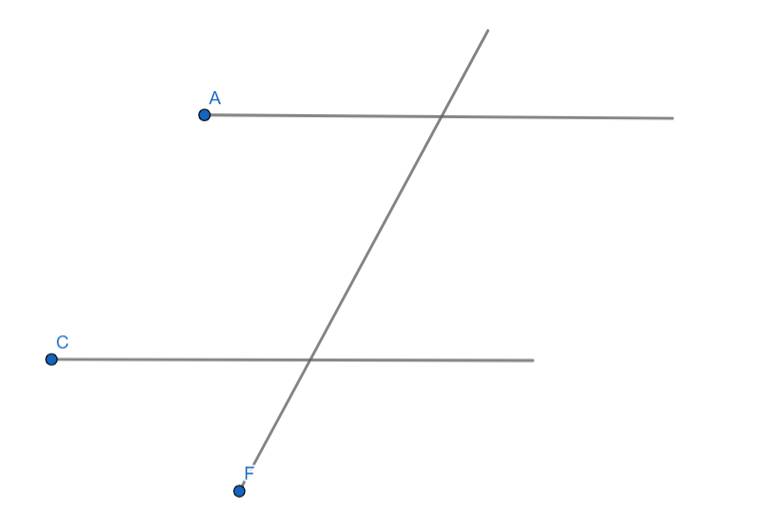
Lúc này ta có: \(A//C\) và \(F\) cắt \(A,C\)
Khi 1 đường thẳng cắt 2 đường thẳng song song sẽ tạp ra các cặp góc: so le trong, đồng vị, trong cùng phía
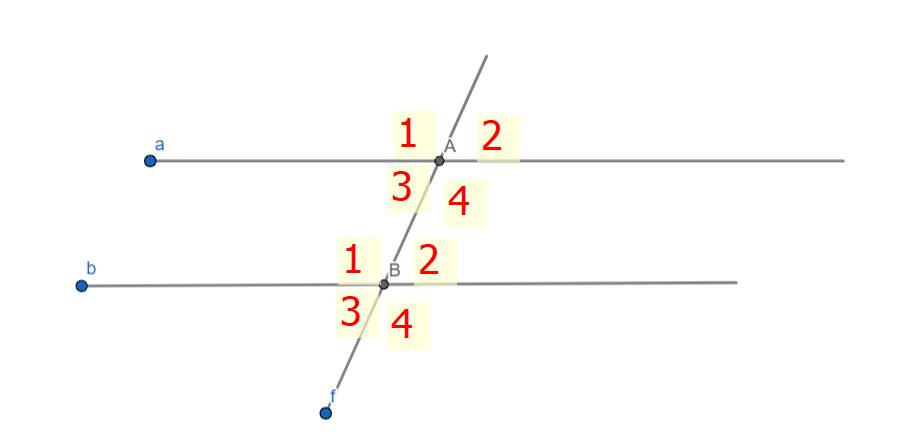
Khai niệm:
Hai góc đồng vị là 2 góc có cùng vị trí trong hai đường thẳng song song bị cắt bởi 1 đường thẳng
- Hai góc đồng vị có cùng số đo với nhau
VD: hai góc đồng vị trong hình:
\(\left(\widehat{A_1};\widehat{B_1}\right);\left(\widehat{A_2};\widehat{B_2}\right);\left(\widehat{A_3};\widehat{B_3}\right);\left(\widehat{A_4};\widehat{B_4}\right)\)
Hai góc so le trong là so le với nhau trong hai đường thẳng song song bị cắt bởi 1 đường thẳng
- Hai góc so le trong có cùng số đo với nhau
VD: hai góc so le trong ở trong hình: \(\left(\widehat{A_3};\widehat{B_2}\right);\left(\widehat{A_4};\widehat{B_1}\right)\)
Hai góc trong cùng phía là hai góc này bên trong 2 đường thẳng và cùng 1 phía trong hai đường thẳng song song bị cắt bởi 1 đường thẳng
- Hai góc trong cùng phía có tổng số đo là 180o
VD: hai góc trong cùng phía trong hình là:
\(\left(\widehat{A_3};\widehat{B_1}\right);\left(\widehat{A};\widehat{B_2}\right)\)
+ Diện tích hình chữ nhật hình vuông, hình tam giác, hình thang; hình bình hành; hình thoi,....
Với:
\(a\): cạnh đáy (chiều dài)
\(b\) :cạnh đáy lớn (chiều rộng)
\(h\): là chiều cao
\(d\): là đường chéo
- Diện tích hình chữ nhật:
\(S=a\times b\)
- Diện tích hình vuông:
\(S=a\times a=a^2\)
- Diện tích hình tam giác:
\(S=\dfrac{1}{2}\times a\times h\)
- Diện tích hình thang:
\(S=\dfrac{a+b}{2}\times h\)
- Diện tích hình bình hành:
\(S=a\times h\)
- Diện tích hình thôi:
\(S=\dfrac{d_1\times d_2}{2}\)
+ Diện tích xung quanh, diện tích toàn phần, thể tích hình hộp chữ nhật, hình lập phương
Với:
\(a\): cạnh (chiều rộng)
\(b\): chiều dài
\(h\): chiều cao
- Diện tích xung quanh của hình hộp chữ nhật:
\(S_{xq}=\left(a+b\right)\times2\times h\)
- Diện tích toàn phần của hình hộp chữ nhật:
\(S_{tp}=S_{xq}+S_đ\times2=\left(a+b\right)\times2\times h+a\times b\times2\)
- Thể tích hình hộp chữ nhật:
\(V=a\times b\times h\)
- Diện tích xung quanh hình lập phương:
\(S_{xq}=\left(a+a\right)\times2\times a=4a^2\)
- Diện tích toàn phần của hình lập phương là:
\(S_{tp}=S_{xq}+S_đ\times2=4a^2+2a^2=6a^2\)
- Thể tích hình lập phương là:
\(V=a\times a\times a=a^3\)
__________________________________________
*Cách học môn toán không bị nhàm chán và thú vi cần biết các tips sau: *
- Không được học liên tiếp 2 - 3 giờ sẽ khiến cho cơ thể mệt mỏi buồn ngủ không hiệu quả
- Để không bị mất gốc thì nên học toàn chú trọng vào các ý chính (VD: ghi nhớ, các điều mà thầy cô lưu ý học)
- Không cần thuộc lòng quan trọng là biết vận dụng vào bài toán
- Cần lưu ý các kiến thức toán cở cấp độ của mình (tiểu học, THCS, THPT)
- Phối hợp việc học toán và việc giải trí tránh bị nhàm chán mất tinh thần
- ....
Các bạn hay anh chị có các tips học toán thú vị hơn mong anh chị bình luận ở đây nhé (trân trọng)
(* Nếu trong part 1 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)
17 tháng 9 2023 lúc 11:45
[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 3) ] |-----------------------------------------------------------------------------|#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị Mất gốc trong môn Toán ở cấp độ THCS (1) Phần số học: + Các tính chất cơ bản giao hoán, kết hợp - Tính chất giao hoán được biểu hiện trong phép cộng và nhân CT: a+b+ca+c+b acdot bcdot cacdot ccdot b Tính chất này khá quen ở cấp tiểu học và rất...
Đọc tiếp
[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 3) ]
|-----------------------------------------------------------------------------|
#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS
(1) Phần số học:
+ Các tính chất cơ bản giao hoán, kết hợp
- Tính chất giao hoán được biểu hiện trong phép cộng và nhân
CT: \(a+b+c=a+c+b\)
\(a\cdot b\cdot c=a\cdot c\cdot b\)
Tính chất này khá quen ở cấp tiểu học và rất quan trọng ở cấp THCS
- Tính chất kết hợp được biểu hiện ở trong phép cộng và nhân
CT: \(a+b+c=\left(a+c\right)+b\)
\(a\cdot b\cdot c=\left(a\cdot c\right)\cdot b\)
Tương tự giao hoán tính chất này rất quan trong để làm các dạng bài tập như:
VD: \(3,12+6+0,88=\left(3,12+0,88\right)+6=4+6=10\)
+ Dấu hiệu chia hết cho các số từ 1 - 10
- Tất cả các số chia hết cho 1
- Chia hết cho 2:
Các số chia hết cho 2 có các chữ số cuối cùng là 0, 2, 4, 6, 8
VD: 12, 56, 96, ...
- Chia hết cho 3:
Dấu hiệu của một số chia hết cho 3 là tổng các chữ số đó sẽ chia hết cho 3:
CT: \(\overline{abcd}\) chia hết cho 3 khi \(a+b+c+d\) chia hết cho 3
VD: \(3210\) chia hết cho 3 vì \(3+2+1+0=6\) ⋮ 3
- Chia hết cho 4:
Dấu hiệu của 1 số chia hết cho 4 khi 2 chữ số cuối cùng của số đó chia hết cho 4 đều này bắt buộc các bạn phải nhớ được các số chia hết cho 4 từ 0 - 99
CT: \(\overline{abcd}\) chia hết cho 4 khi \(\overline{cd}\) chia hết cho 4
VD: \(3456\) chia hết cho 4 khi 56 chia hết cho 4
- Chia hết cho 5:
Dấu hiệu chia hết cho 5 là các số có chữ số cuối cùng là 5 hoặc 0
- Chia hết cho 6:
Dấu hiệu của một số chia hết cho 6 là số đó vừa chia hết cho 2 vừa chia hết cho 3
VD: 1230 chia hết cho 6 vì 1230 vừa chia hết cho 2 vừa chia hết cho 3
- Chia hết cho 7:
Dấu hiệu của 1 số chia hết cho 7 là lấy 5 nhân cho chữ số tận cùng rồi cộng cho phần còn lại của số đó nếu chia hết cho 7 thì số đó chia hết cho 7
CT: \(\overline{abcd}\)chia hết cho 7 khi \(5\cdot d+\overline{abc}\) ⋮ 7
VD: 182 chia hết cho 7 vì \(5\cdot2+18=28\) ⋮ 7
- Chia hết cho 8
Dấu hiệu 1 số chia hết cho 8 khi 3 chữ số cuối của số đó chia hết cho 8
VD: 1264 chia hết cho 8 khi 3 chữ số cuối của nó chia hết cho 8
- Chia hết cho 9
Dấu hiệu của 1 số chia hết cho 9 khi tổng các chữ số của số đó tạo thành 1 số chia hết cho 4
CT: \(\overline{abcd}\) chia hết cho 8 khi \(a+b+c+d\) ⋮ 9
VD: 36 chia hết cho 9 vì 3 + 6 chia hết cho 9
- Chia hết cho 10
Dấu hiệu chia hết cho 10 là chữ số tận cùng của số đó là số 0
VD: 120 chia hết cho 10 vì có chữ số tận cùng là số 0
+ Quy tắc dấu của các phép cộng trừ nhân chia các số nguyên
- Phép cộng:
\(a+b=a+b\)
\(\left(-a\right)+\left(-b\right)=-\left(a+b\right)\)
\(a+\left(-b\right)=a-b\)
\(-a+b=b-a\)
- Phép trừ:
\(a-b=a-b\)
\(-a-b=-\left(a+b\right)\)
\(a-\left(-b\right)=a+b\)
- Phép nhân:
\(a\cdot b=a\cdot b\)
\(-a\cdot-b=a\cdot b\)
\(a\cdot-b=-\left(a\cdot b\right)\)
\(-a\cdot b=-\left(a\cdot b\right)\)
- Phép chia:
\(a:b=a:b\)
\(-a:-b=a:b\)
\(-a:b=-\left(a:b\right)\)
\(a:-b=-\left(a:b\right)\)
Lưu ý: Khi mở/ đóng ngoặc nếu trước dấu ngoặc đó là dấu + thì dữ nguyên nếu trước dấu ngoặc đó là dấu - thì đổi dấu tất cả hạng tử của phép tính đó:
VD: \(-\left(a-b-c\right)=-a+b+c\)
+ Tính chất dãy tỉ số bằng nhau
Ta có tính chất này:
Nếu: \(\dfrac{a}{m}=\dfrac{b}{n}\) (với m,n là số nguyên ≠ biến) và biết \(a\pm b=?\) thì ta có thể tìm được a,b như sau:
VD: \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{a+b}{2+3}=\dfrac{5}{5}=1\) (biết \(a+b=5\))
\(\Rightarrow\left\{{}\begin{matrix}a=2\cdot1=2\\b=3\cdot1=3\end{matrix}\right.\)
Công thức tổng quát: \(\dfrac{a_1}{m_1}=\dfrac{a_2}{m_2}=\dfrac{a_3}{m_3}=...=\dfrac{a_n}{m_n}=\dfrac{a_1+a_2+...+a_n}{m_1+m_2+...+m_n}\)
(2) Phần hình học
+ Các trường hợp bằng nhau của tam giác
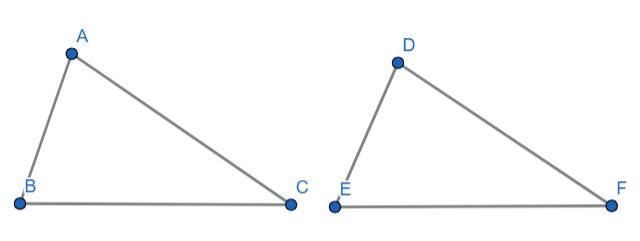
- Trường hợp 1:
Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì 2 tam giác này bằng nhau
Xét ΔABC và ΔDEF ta có:
\(AB=DE\left(gt\right)\)
\(AC=DF\left(gt\right)\)
\(BC=EF\left(gt\right)\)
\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(c.c.c\right)\)
- Trường hợp 2:
Nếu 2 cạnh của tam giác này bằng 2 cạnh của tam giác kia và 1 góc nằm giữa 2 cạnh này của tam giác này bằng góc nằm giữa 2 cạnh này của tam giác kia thì hai tam giác bằng nhau
Xét ΔABC và ΔDEF ta có:
\(AB=DE\left(gt\right)\)
\(AC=DF\left(gt\right)\)
\(\widehat{A}=\widehat{D}\left(gt\right)\)
\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(c.g.c\right)\)
- Trường hợp 3:
Nếu 1 cạnh của tam giác này bằng 1 cạnh của tam giác kia và 2 góc kề cạnh này của tam giác này bằng 2 góc kề cạnh này của tam giác kia thì hai tam giác bằng nhau
Xét ΔABC và ΔDEF ta có:
\(\widehat{A}=\widehat{D}\left(gt\right)\)
\(AB=DE\left(gt\right)\)
\(\widehat{B}=\widehat{E}\left(gt\right)\)
\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(g.c.g\right)\)
+ Định lý Py-ta-go thuận và đảo
- Theo định lý Py-ta-go thì trong 1 tam giác vuông thì tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền (nhận biết cạnh huyền: cạnh đối diện với góc vuông thì cạnh đó là cạnh huyền
Theo ĐL Py-ta-go trong tam giác vuông: \(a^2+b^2=c^2\) (1) (a,b là cạnh góc vuông, c là cạnh huyền)
Từ công thức thên ta có thể tính được toàn bộ các cạnh của tam giác vuông khi biết 2 cạnh còn lại
Từ (1) \(\Rightarrow\left\{{}\begin{matrix}c=\sqrt{a^2+b^2}\\a=\sqrt{c^2-b^2}\\b=\sqrt{c^2-a^2}\end{matrix}\right.\)
- Định lý Py-ta-go đảo được dựa trên định lý Py-ta-go thuận nên nếu trong 1 tam giác bình phương của cạnh này bằng tổng bình phương của 2 cạnh còn lại thì tam giác đó là tam giác vuông (góc đối diện với cạnh bằng tổng bình phương hai cạnh kia chính là góc vuông)
Theo định lý Py-ta-go đảo: \(c^2=a^2+b^2\Rightarrow\text{Δ}\) đó vuông
VD: Cho tam giác ABC vuông tại A và AB=3(cm), AC=4(cm). Tính BC
Xét ΔABC vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC^2=AC^2+AB^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=\sqrt{25}=5\left(cm\right)\)
+ Bộ 3 độ dài cạnh của tam giác
Để xác định được bộ 3 độ dài cạnh của tam giác thì ta có nhận xét sau:
\(\left\{{}\begin{matrix}a+b>c\\a+c>b\\b+c>a\end{matrix}\right.\Rightarrow a,b,c\) là bộ 3 độ dài cạnh của tam giác
VD: cho tam giác ABC có: AB = 1(cm), AC=1,5(cm), BC=5(cm)
Ta có:
\(\left\{{}\begin{matrix}AB+AC< BC\left(1+1,5< 5\right)\\BC+AB>AC\left(1+5>15\right)\\BC+AC>AB\left(5+1,5>1\right)\end{matrix}\right.\)
Vậy bộ 3 độ dài của của tam giác ABC là không đúng
________________________________________
*Cách học môn toán không bị nhàm chán và thú vi cần biết các tips sau: *
- Không được học liên tiếp 2 - 3 giờ sẽ khiến cho cơ thể mệt mỏi buồn ngủ không hiệu quả
- Để không bị mất gốc thì nên học toàn chú trọng vào các ý chính (VD: ghi nhớ, các điều mà thầy cô lưu ý học)
- Không cần thuộc lòng quan trọng là biết vận dụng vào bài toán
- Cần lưu ý các kiến thức toán cở cấp độ của mình (tiểu học, THCS, THPT)
- Phối hợp việc học toán và việc giải trí tránh bị nhàm chán mất tinh thần
- Sử dụng sơ đồ tư duy, takennotes, ...
- Lại đi làm lại nhiều lần dạng bài còn yếu
- Ôn lại nhiều lần các kiến thức, khái niệm, công thức...
- Sử dụng nhiều kĩ thuật nhớ lâu, nhanh
Các bạn hay anh chị có các tips học toán thú vị hơn mong anh chị bình luận ở đây nhé (trân trọng)
(* Nếu trong part 3 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)