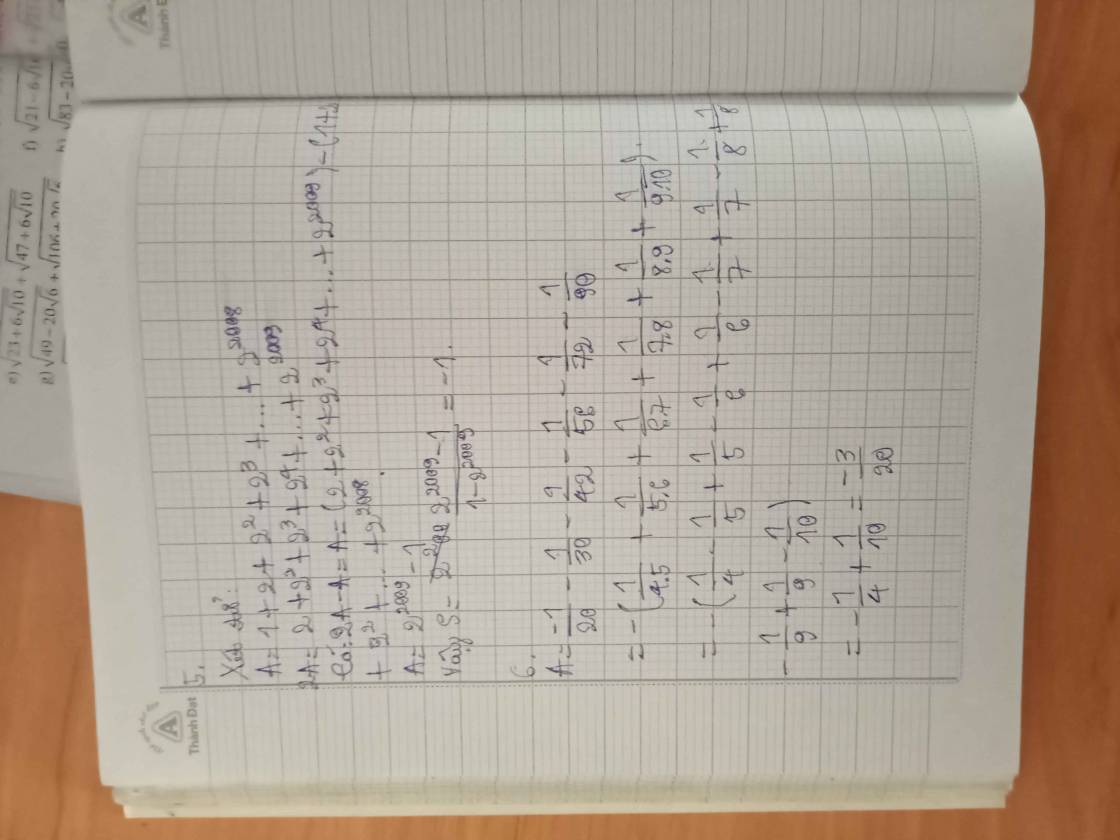
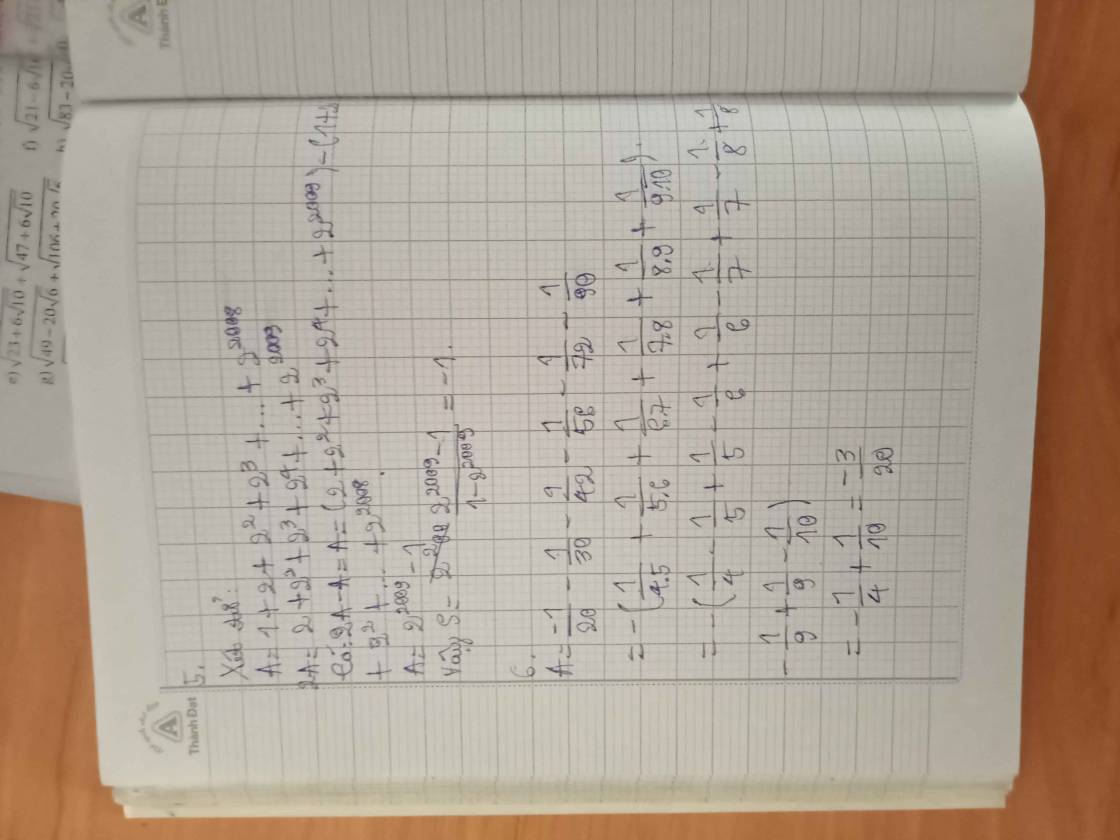
6:
\(A=-\left(\dfrac{1}{20}+\dfrac{1}{30}+...+\dfrac{1}{90}\right)\)
=-(1/4-1/5+1/5-1/6+...+1/9-1/10)
=-1/4+1/10
=-5/20+2/20=-3/20
Bài 6 :
\(A=\dfrac{-1}{20}+\dfrac{-1}{30}+\dfrac{-1}{42}+\dfrac{-1}{56}+\dfrac{-1}{72}+\dfrac{-1}{90}\\ =\dfrac{-1}{4\cdot5}+\dfrac{-1}{5\cdot6}+...+\dfrac{-1}{9\cdot10}\\ =-1\cdot\left(\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{9\cdot10}\right)\\ =-1\cdot\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\\ =-1\cdot\left(\dfrac{1}{4}-\dfrac{1}{10}\right)=-\dfrac{1}{40}\)
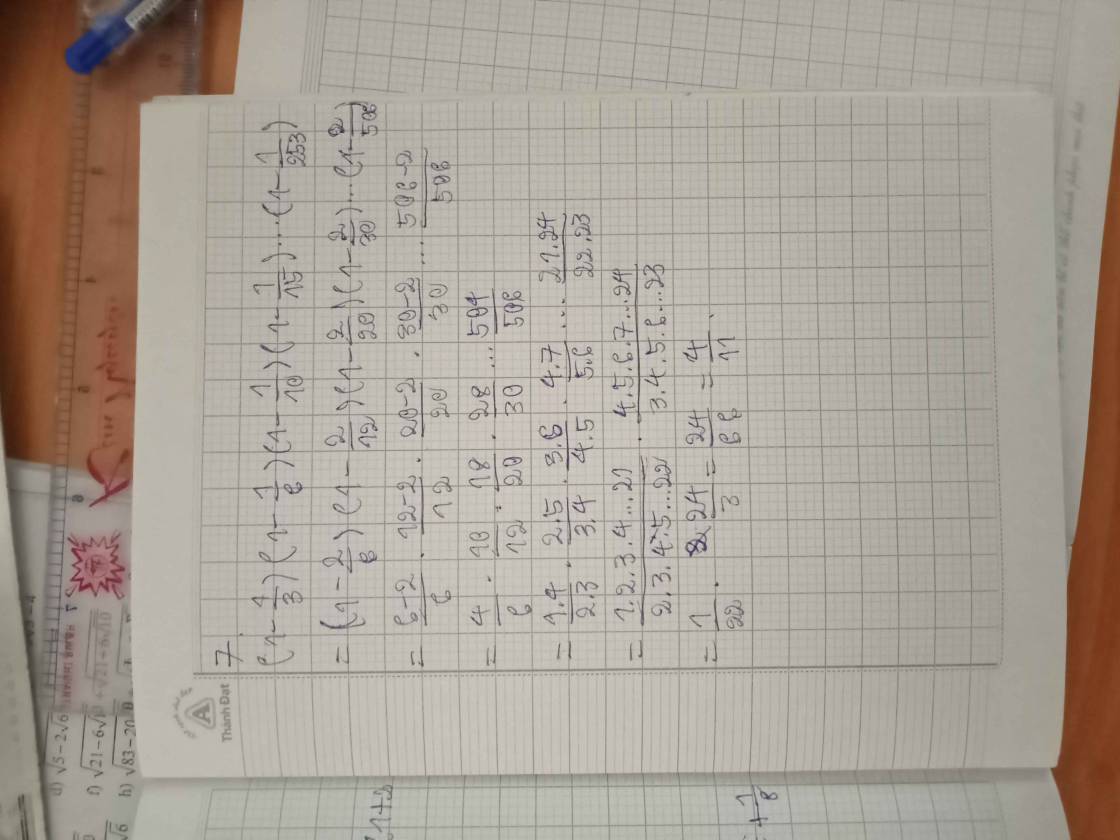
Bài 7 :
\(\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)\left(1-\dfrac{1}{15}\right)...\left(1-\dfrac{1}{253}\right)\\ =\dfrac{2}{3}\cdot\dfrac{5}{6}\cdot\dfrac{9}{10}\cdot\dfrac{14}{15}...\cdot\dfrac{252}{253}\\ =\dfrac{4}{6}\cdot\dfrac{10}{12}\cdot\dfrac{18}{20}\cdot\dfrac{28}{30}...\cdot\dfrac{504}{506}\\ =\dfrac{1\cdot4}{2\cdot3}\cdot\dfrac{2\cdot5}{3\cdot4}\cdot\dfrac{3\cdot6}{4\cdot5}\cdot\dfrac{4\cdot7}{5\cdot6}\cdot...\cdot\dfrac{21\cdot24}{22\cdot23}\\ =\dfrac{1\cdot2\cdot3\cdot4^2\cdot5^2\cdot...\cdot21^2\cdot22\cdot23\cdot24}{2\cdot3^2\cdot4^2\cdot...\cdot22^2\cdot23}\\ =\dfrac{1\cdot24}{3\cdot22}=\dfrac{4}{11}\)


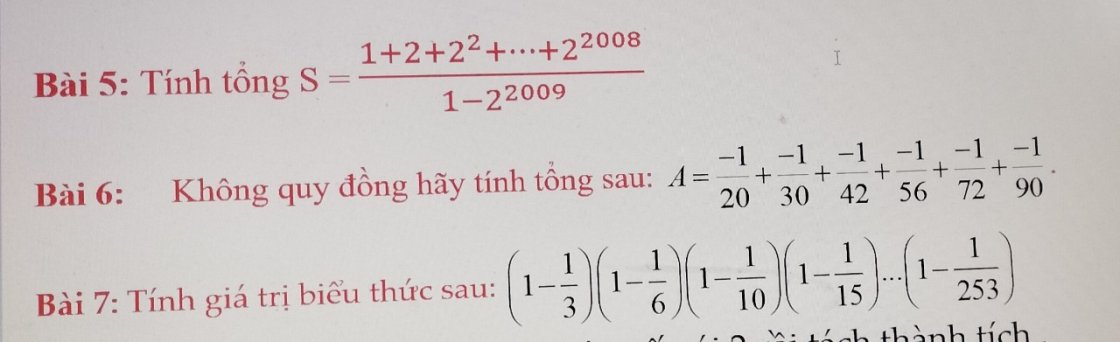 các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm









 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ

 giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ

 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
