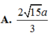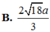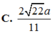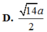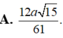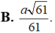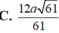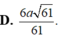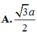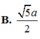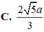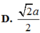c1: viets phương trinh tiếp tuyến của đồ thị hàm số \(y=x^3+4x+2\) tại điểm có hoành độ bằng -1
c2: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh 2a. hình chiếu vuông góc của S lên (ABCD) trùng với trung điểm H của AD,chiều cao SH bằng 2a
a, chứng minh đường thẳng ab vuông góc với mặt phẳng SAD
b, tính khoảng cách giữa hai đường thẳng BD và SC
c1: \(y=x^3+4x+2\)
\(\Rightarrow y'=3x^2+4\)
Ta có: \(x_0=-1\Rightarrow y_0=-3\)
\(\Rightarrow f'\left(x_0\right)=7\)
\(\Rightarrow\) Phương trình tiếp tuyến: \(y+3=7\left(x+1\right)\)
\(\Leftrightarrow y=7x+4\)