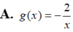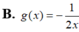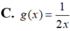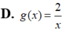Các câu hỏi tương tự
Cho F'(x) = f(x), C là hằng số dương tùy ý.
Khi đó ∫ f(x)dx bằng:
A. F(x) + C B. F(x) - C
C. F(x) + lnC D. F(x + C)
Cho F'(x) = f(x), C là hằng số dương tùy ý.
Khi đó 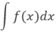 bằng:
bằng:
A. F(x) + C B. F(x) - C
C. F(x) + lnC D. F(x + C)
∫
x
+
1
.
s
i
n
x
d
x
bằng:A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + CC. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Đọc tiếp
∫ x + 1 . s i n x d x bằng:
A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + C
C. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
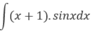 bằng:
bằng:
A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + C
C. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Biết
∫
f
(
x
-
1
)
d
x
x
-
1
x
+
1
+c và
∫
f
(
x
+
1
)
d
x
F
(
x
)
+
c
thì
Đọc tiếp
Biết ∫ f ( x - 1 ) d x = x - 1 x + 1 +c và ∫ f ( x + 1 ) d x = F ( x ) + c thì
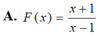
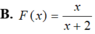
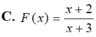
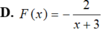
Giả sử
∫
2
x
+
3
x
(
x
+
1
)
(
x
+
2
)
(
x
+
3
)
+
...
Đọc tiếp
Giả sử ∫ 2 x + 3 x ( x + 1 ) ( x + 2 ) ( x + 3 ) + 1 d x = - 1 g ( x ) + C (C là hằng số). Tính tổng của các nghiệm của phương trình g(x) = 0
A. -1
B. 1
C. 3
D. -3
∫
x
x
-
1
d
x
bằng:A.
x
-
1
5
2
+
x
-
1
3
2...
Đọc tiếp
∫ x x - 1 d x bằng:
A. x - 1 5 2 + x - 1 3 2 + C
B. 2 15 3 x - 1 5 2 - 5 x - 1 3 2 + C
C. 2 15 3 x - 1 5 2 + 5 x - 1 3 2 + C
D. 1 15 3 x - 1 5 2 + 5 x - 1 3 2 + C
Cho (C): y=(x+1)(x-2)(x-m). Xác định m ∈ ℝ để (C) có cực đại, cực tiểu
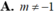
![]()
![]()
![]()
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn
f
(
x
)
.
f
(
a
-
x
)
1...
Đọc tiếp
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn f ( x ) . f ( a - x ) = 1 f ( x ) > 0 ; ∀ x ∈ [ 0 ; a ] và ∫ 0 a d x 1 + f ( x ) = b a c , trong đó b, c là hai số nguyên dương và b/c là phân số tối giản. Khi đó b+c có giá trị thuộc khoảng nào dưới đây?
A. (11;22)
B. (0;9)
C. (7;21)
D. (2017;2020)
Cho
(
C
)
:
y
2
x
biết
(
C
1
)
:
y
g
(
x
)
đối xứng với (C) qua (d):x+y0. Tìm g(x).
Đọc tiếp
Cho ( C ) : y = 2 x biết ( C 1 ) : y = g ( x ) đối xứng với (C) qua (d):x+y=0. Tìm g(x).