Đáp án A.
Ta có:
x − 3 x 2 − 2 x + 1 = x − 1 − 2 x − 1 2 = 1 x − 1 − 2 x − 1 2 ⇒ ∫ x − 3 x 2 − 2 x + 1 d x = ∫ 1 x − 1 − 2 x − 1 2 d x
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hàm số
y
f
x
xác định, liên tục và có đạo hàm trên đoạn
a
,
b
.
Xét các khẳng định sau: 1. Hàm số
f
x
đồng biến trên
a
;
b
thì
f
x
0
,
∀
x
∈...
Đọc tiếp
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Cho hàm số f(x)có đồ thị là đường cong (C)biết đồ thi ̣của f(x)như hình vẽ. Tiếp tuyến của (C) tại điểm có hoành độ bằng 1 cắt đồ thi ̣ (C) tại hai điểm A, B phân biệt lần lượt có hoành độ a, b. Chọn khẳng định đúng trong các khẳng định sau A.
4
≥
a
−
b
≥
−
4
B.
a
−
b
≥
0
C.
a
,
b
3...
Đọc tiếp
Cho hàm số f(x)có đồ thị là đường cong (C)biết đồ thi ̣của f'(x)như hình vẽ. Tiếp tuyến của (C) tại điểm có hoành độ bằng 1 cắt đồ thi ̣ (C) tại hai điểm A, B phân biệt lần lượt có hoành độ a, b. Chọn khẳng định đúng trong các khẳng định sau
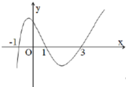
A. 4 ≥ a − b ≥ − 4
B. a − b ≥ 0
C. a , b < 3
D. a 2 + b 2 > 10
Cho hàm số f(x) liên tục trên R,
f
x
≠
0
với mọi x và thỏa mãn
f
1
−
1
2
,
f
x
2
x
+
1
f
2
x
. Biết
f
1
+
f...
Đọc tiếp
Cho hàm số f(x) liên tục trên R, f x ≠ 0 với mọi x và thỏa mãn f 1 = − 1 2 , f ' x = 2 x + 1 f 2 x . Biết f 1 + f 2 + ... + f 2019 = a b − 1 v ớ i a ∈ ℤ , b ∈ ℕ , a ; b = 1 . Khẳng định nào sau đây là sai?
A. a − b = 2019
B. ab > 2019
C. 2 a + b = 2022
D. b ≤ 2020
Cho hàm số
y
f
(
x
)
c
ó
f
(
x
)
0
,
∀
x
∈
(
a
,
b
)
Chọn khẳng định đúng trong các khẳng định sau: A. Hàm số đồng biến trên
(
a
,
b
)
B. Hàm số nghịch biến trên
(
a
,...
Đọc tiếp
Cho hàm số y = f ( x ) c ó f ' ( x ) > 0 , ∀ x ∈ ( a , b ) Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số đồng biến trên ( a , b )
B. Hàm số nghịch biến trên ( a , b )
C. Hàm số nhận giá trị không đổi trên ( a , b )
D. Hàm số đồng biến trên ℝ
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn (
[
f
(
x
)
]
2
[
f
(
x
)
]
2...
Đọc tiếp
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn ( [ f ( x ) ] 2 [ f ' ( x ) ] 2 ) e 2 x = 1 + [ f ( x ) ] 2 và f(x)> 0 với ∀x∈[0;1], biết f(0)=1. hãy chọn khẳng định đúng trong các khẳng định sau
A. 5 2 <f(1)< 3
B. 3<f(1)< 7 2
C. 2<f(1)< 5 2
D. 3 2 <f(1)< 2
Cho hàm số yf(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:1) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;
b
thì
f
x
o
là giá trị lớn nhất của f(x) trên đoạn [a;b]2) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số yf(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:1) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;
b
thì
f
x
o
là giá trị lớn nhất của f(x) trên đoạn[a,b]2) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;...
Đọc tiếp
Cho hàm số y=f(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn[a,b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số yf(x) liên tục và có đạo hàm tới cấp hai trên a,b ;
x
0
∈
a
;
b
. Chọn khẳng định đúng trong các khẳng định sau: A. Nếu
f
x
0
0...
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đạo hàm tới cấp hai trên a,b ; x 0 ∈ a ; b . Chọn khẳng định đúng trong các khẳng định sau:
A. Nếu f ' x 0 = 0 f ' ' x 0 < 0 thì x 0 là một điểm cực tiểu của hàm số
B. Nếu f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x 0 là một điểm cực trị của hàm số.
C. Nếu f ' x 0 = 0 f ' ' x 0 > 0 thì x 0 là một điểm cực đại của hàm số
D. A, B, C đều sai.
Cho hàm số
f
x
8
x
4
+
a
x
2
+
b
,
trong đó a, b là các tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn
[
-
1
;
1
]
bằng 1. Hãy chọn khẳng định đúng A. a 0,b 0 B. a 0...
Đọc tiếp
Cho hàm số f x = 8 x 4 + a x 2 + b , trong đó a, b là các tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [ - 1 ; 1 ] bằng 1. Hãy chọn khẳng định đúng
A. a < 0,b < 0
B. a > 0,b > 0
C. a < 0,b > 0
D. a > 0,b < 0