Gọi S’ là giá trị của S khi giảm đi 16 lần, x’ là cạnh hình lập phương khi S giảm đi 16 lần.
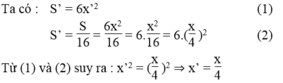
Vậy khi S giảm đi 16 lần thì cạnh hình vuông giảm đi 4 lần.
Gọi S’ là giá trị của S khi giảm đi 16 lần, x’ là cạnh hình lập phương khi S giảm đi 16 lần.
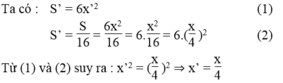
Vậy khi S giảm đi 16 lần thì cạnh hình vuông giảm đi 4 lần.
Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
Nhận xét sự tăng, giảm của S khi x tăng.
Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
Tính cạnh của hình lập phương khi S = 27/2 c m 2 , S = 5 c m 2
Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
Biểu diễn diện tích toàn phần S (tức là tổng diện tích của sáu mặt) của hình lập phương qua x.
Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
| x | 1/3 | 1/2 | 1 | 3/2 | 2 | 3 |
| S |
Ông Cường có 2 thùng rượu hình lập phương có độ dài cạnh lần lượt là \(x,y\left(x,y>0\right)\). Ông Dũng cũng có 2 thùng rượu hình hộp chữ nhật, thùng thứ nhất có đáy là hình vuông cạnh a, chiều cao b; thùng thứ hai có đáy là hình vuông cạnh b, chiều cao a. Hỏi ông Cường và ông Dũng, ai sở hữu lượng rượu nhiều hơn? Biết rằng các thùng đều chứa đầy rượu.
Giải bài toán sau bằng cách lập hệ phương trình:
Hình A là hình chữ nhật, hình B là hình vuông. Hai hình A và B có chu vi bằng nhau. Diện tích hình B lớn hơn diện thích hình A là \(1cm^2\). Nếu tăng độ dài cạnh hình vuông thêm 3cm, tăng chiều rộng thêm 1cm và giảm chiều dài 1 đoạn là 3cm của A thì lúc này diện tích hình B lớn hơn diện tích hình A là \(65cm^2\). Tìm độ dài đường chéo hình chữ nhật
ai giúp mk vs!!!
Giải bài toán bằng cách lập phương trình:
1 thửa ruộng hình chữ nhật có S=100m2.Tính độ dài các cạnh của thửa ruộng.Bt rằng nếu tăng chiều rộng lên 2 m và giảm chiều dài đi 5m thì S tăng thêm 5m2
Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.
Nếu bán kính tăng gấp 3 lần thì diện tích tăng hay giảm bao nhiêu lần?
Cho một tam giác vuông với cạnh huyền có chiều dài c, độ dài hai cạnh góc vuông lần lượt là a và b \(\left(c>a,b>0\right)\). Từ a và b ta lập 2 hình chữ nhật đều có độ dài hai kích thước là a và b. Chứng minh rằng diện tích của hình vuông cạnh c luôn lớn hơn hoặc bằng tổng diện tích của 2 hình chữ nhật vừa lập được. Tam giác vuông ban đầu cần có thêm điều kiện gì để trường hợp bằng xảy ra?