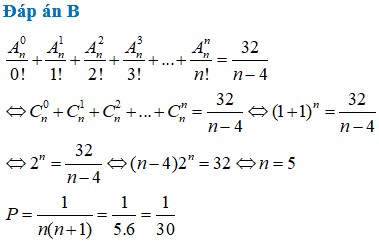Các câu hỏi tương tự
Cho các số thực a, b, m, n sao cho
2
m
+
n
0
và thỏa mãn điều kiện
log
2
a
2
+
b
2
+...
Đọc tiếp
Cho các số thực a, b, m, n sao cho 2 m + n < 0 và thỏa mãn điều kiện log 2 a 2 + b 2 + 9 = 1 + log 2 3 a + 2 b 9 − m .3 − n .3 − 4 2 m + n + ln 2 m + n + 2 2 + 1 = 81
Tìm giá trị nhỏ nhất của biểu thức P = a − m 2 + b − n 2
A. 2 5 − 2.
B. 2.
C. 5 − 2.
D. 2 5 .
Biết
n
∈
ℤ
+
,
n
4
và thỏa mãn
A
n
0
0
!
+
A
n
1
1
!
+
A
n
2
2...
Đọc tiếp
Biết n ∈ ℤ + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + A n 2 2 ! + A n 3 3 ! + . . . + A n n n ! = 32 n - 4 . Tính P = 1 n n + 1
A. P = 1 42
B. P = 1 30
C. P = 1 56
D. P = 1 72
Cho n số a1,a2,......,an biết rằng mỗi số trong chúng bằng 1 hoặc -1 và:
a1.a2+a2.a3+..........+an-1.an+an.a1=0
C/m n chia hết cho 4
giải pt
\(C^4_{n-1}-C^3_{n-1}-\frac{5}{4}A^2_{n-2}=0\)
Cho a, b 0 thỏa mãn điều kiện a + b + ab 1, giá trị nhỏ nhất của
P
a
4
+
b
4
l
à
x
(
x
-
y
)
4
(
x
,
y
∈
N
)
. Giá trị của x + y là A. 3 B. 5 C. 7 D. 9
Đọc tiếp
Cho a, b > 0 thỏa mãn điều kiện a + b + ab = 1, giá trị nhỏ nhất của P = a 4 + b 4 l à x ( x - y ) 4 ( x , y ∈ N ) . Giá trị của x + y là
A. 3
B. 5
C. 7
D. 9
Cho số phức
z
1
+
i
n
, biết
n
∈
ℤ
và thỏa mãn
log
2
8
−
n
+
log
2
n
+
3
log
2...
Đọc tiếp
Cho số phức z = 1 + i n , biết n ∈ ℤ và thỏa mãn log 2 8 − n + log 2 n + 3 = log 2 10
Tính môđun của số phức z
A. 8
B. z = 8 2 hoặc z = 1 2
C. 4 2
D. 2
1: cho phân số a phần b <1 ( a,b thuộc N , b không bằng 0)
so sánh a phần b với a + n phần b+n
2: cho phân số a phần b >1 (a,b thuộc N, b không bằng 0)
so sánh a phần b với a+n phần b+n
3: cho A=20032003 +1 phần 20032004 +1
và B= 20032002 +1 phần 20032004 +1
so sánh a và b
Cho n, k là những số nguyên thỏa mãn
0
≤
k
≤
n
v
à
n
≥
1
Tìm khẳng định sai. A.
P
n
A
n
n
B.
C
n
k
C
n
n
−
k
C. ...
Đọc tiếp
Cho n, k là những số nguyên thỏa mãn 0 ≤ k ≤ n v à n ≥ 1 Tìm khẳng định sai.
A. P n = A n n
B. C n k = C n n − k
C. A n k = n ! k !
D. P k . C n k = A n k
Với n thuộc Z các số sau là chẵn hay lẻ:
A=(n-4)(n-15)
B=n^2-n-1