Đáp án: A
A ∩ B = ∅ => Các phần tử thuộc A thì không thuộc B nên số phần tử của bằng tổng số phần tử của A và B.
=> I đúng.
II và III sai vì khi ±|A ∩ B| = ∅ làm thay đổi tổng số phần tử của A và B.
Biết |A| là kí hiệu chỉ số phần tử của tập hợp A. Trong các bất đẳng thức sau
I. A ∩ B ≤ A ≤ A ∪ B
II. A ∩ B ≤ A < A ∪ B
III. A \ B < A ∪ B ≤ A + B
Bất đẳng thức đúng là:
A. Chỉ I.
B. Chỉ I và II.
C. Chỉ II và III.
D. Cả I, II và III.
Cho hai tập hợp A, B. Xét các mệnh đề sau:
(I) ( A ∩ B ) ∪ A = A
(II) ( A ∪ B ) ∩ B = B
(III) ( A \ B ) ∩ ( B \ A ) = ∅
(IV) ( A \ B ) ∪ B = A ∪ B
Hỏi có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 4
B. 3
C. 2
D.1
Cho a, b, c, d là các số thực thỏa mãn a < b < c < d và các mệnh đề sau:
(I) ( a ; b ) ∩ ( c ; d ) = ∅
(II) ( a ; c ] ∩ [ b ; d ) = ( b ; c )
(III) ( a ; c ] ∪ ( b ; d ] = ( a ; d ]
(IV) ( − ∞ ; b ) \ ( a ; d ) = ( − ∞ ; a ]
(V) ( b ; d ) \ ( a ; c ) = ( c ; d )
(VI) ( a ; d ) \ ( b ; c ) = ( a ; b ] ∪ [ c ; d )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 5
B. 4
C. 3
D. 2
Cho tập hợp A={1, 2, 3, 4, a, b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3, 4} ∈ A”.
(III): “{a, 3, b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng
A. I đúng
B. I,II đúng
B. I,II đúng
B. I,II đúng
Xét hai tập hợp A, B bất kì và các khẳng định sau:
(I) ( A ∪ B ) ⊂ B
(II) ( A ∩ B ) ⊂ A
(III) A ⊂ ( A ∪ B )
(IV) ( A ∩ B ) ⊂ ( A ∪ B )
(V) A \ B = B \ A
(VI) A \ B ⊂ A
Trong các khẳng định trên, có bao nhiêu khẳng định là mệnh đề đúng?
A. 2
B. 3
C. 4
D. 5
Xét hai tập hợp A, B và các khẳng định sau:
(I) Nếu B ⊂ A thì A ∩ B = B
(II) Nếu A ⊂ B thì A ∪ B = A
(III) Nếu B ⊂ A ( B ≠ A ) thì A \ B = ∅
(IV) Nếu A ∩ B = ∅ thì A \ B = A
Trong các khẳng định trên, có bao nhiêu khẳng định là mệnh đề đúng?
A. 1
B. 2
C. 3
D. 4
Cho x là một phần tử của tập hợp A. Xét các mệnh đề sau:
(I) x ∈ A
(II) x ∈ A
(III) x ⊂ A
(IV) x ⊂ A
Trong các mệnh đề trên, mệnh đề nào đúng?
A. I và II
B. I và III
C. I và IV
D. II và IV
Cho A và B là hai tập hợp con của tập hợp E được biểu diễn bởi biểu đồ Ven dưới đây
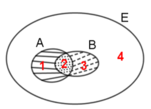
Trong các phát biểu sau
I. Vùng 1 là tập hợp A \ B.
II. Vùng 2 là tập hợp A ∩ B.
III. Vùng 3 là tập hợp B \ A.
IV. Vùng 4 là tập hợp E \ (A ∪ B).
Số phát biểu đúng là:
A. 1.
B. 2.
C. 3.
D. 4.
Cho các khẳng định sau: (I): \(N\cap Z=N\) (II): R\Q = Z (III): Q \(\cup R=R\) (IV): \(Q\cup N\)* = N*
Trong các khẳng định sau có bao nhiêu khẳng định là mệnh đề đúng?
