Các câu hỏi tương tự
Biết
1
+
i
+
i
2
+
.
.
.
.
+
i
100
a
+
b
i
(
a
,
b
∈
ℝ
)
. Tìm a,b.
A
.
...
Đọc tiếp
Biết 1 + i + i 2 + . . . . + i 100 = a + b i ( a , b ∈ ℝ ) . Tìm a,b.
A . a = 0 b = 1
B . a = 1 b = 0
C . a = 1 b = 1
D . a = - 1 b = - 1
Cho số phức z a + bi(a,b
∈
ℝ
). Biết {M} biểu diễn số phức z là đường tròn
x
-
4
2
+
y
-
3
2
9
. Tìm max, min của F 4a + 3b. A.
m...
Đọc tiếp
Cho số phức z = a + bi(a,b ∈ ℝ ). Biết {M} biểu diễn số phức z là đường tròn x - 4 2 + y - 3 2 = 9 . Tìm max, min của F = 4a + 3b.
A. m a x F = 28 m i n F = 13
B. m a x F = 50 m i n F = 13
C. m a x F = 40 m i n F = 10
D. m a x F = 30 m i n F = 10
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức
z
a
+
b
i
(
a
,
b
∈
ℝ
)
thỏa mãn
z
-
1
z...
Đọc tiếp
Cho số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn z - 1 z - i = 1 và z - 3 i z + i = 1 .Tính P=a+b.
A. P=7
B. P=-1
C. P=1
D. P=2
Biết
∫
1
3
d
x
1
+
x
+
1
+
x
2
a
3
+
b
2
+
c
+
1
2...
Đọc tiếp
Biết ∫ 1 3 d x 1 + x + 1 + x 2 = a 3 + b 2 + c + 1 2 ln ( 3 2 - 3 ) với a, b, c là các số hữu tỷ.
Tính P = a + b + c.
![]()
![]()
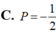
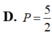
Với các số nguyên a,b thỏa mãn
∫
1
2
(
2
x
+
1
)
ln
x
d
x
a
+
3
2
+
ln
b
tính tổng a+b A. P 27 B. P 28 C. P 60 D. P 61
Đọc tiếp
Với các số nguyên a,b thỏa mãn ∫ 1 2 ( 2 x + 1 ) ln x d x = a + 3 2 + ln b tính tổng a+b
A. P = 27
B. P = 28
C. P = 60
D. P = 61
Cho số phức z1+i. Biết rằng tồn tại các số phức
z
1
a
+
5
i
,
z
2
b
(trong đó
a
,
b
∈
ℝ...
Đọc tiếp
Cho số phức z=1+i. Biết rằng tồn tại các số phức z 1 = a + 5 i , z 2 = b
(trong đó a , b ∈ ℝ , b > 1 ) thỏa mãn 3 z - z 1 = 3 z - z 2 = z 1 - z 2 .
Tính b-a.
A. ![]()
B. ![]()
C. ![]()
D. ![]()



