Các câu hỏi tương tự
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y
x
,y0 và x4 quanh trục Ox. Đường thẳng xa (0a4) cắt đồ thị hàm số
y
x
tại M (hình vẽ bên). Gọi
V
1
là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V2
V
1
. Khi đó A. a
2...
Đọc tiếp
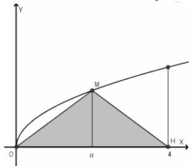
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x ,y=0 và x=4 quanh trục Ox. Đường thẳng x=a (0<a<4) cắt đồ thị hàm số y = x tại M (hình vẽ bên). Gọi V 1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V=2 V 1 . Khi đó
A. a = 2 2
B. a = 5 2
C. a = 2
D. a = 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
2
2
, cạnh bên SA vuông góc với mặt phẳng đáy và SA3 Mặt phẳng
α
qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP. A.
V
64
2
π
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3 Mặt phẳng α qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
A. V = 64 2 π 3
B. V = 125 π 6
C. V = 32 π 3
D. V = 10 Sπ 3
Cho hình chóp đều S.ABCD, đáy ABCD là hình vuông cạnh a, các cạnh bên tạo với đáy góc 45 độ. Diện tích toàn phần của hình chóp trên theo a là. A.
2
3
a
2
B.
3
+
1
a
2
C. ...
Đọc tiếp
Cho hình chóp đều S.ABCD, đáy ABCD là hình vuông cạnh a, các cạnh bên tạo với đáy góc 45 độ. Diện tích toàn phần của hình chóp trên theo a là.
A. 2 3 a 2
B. 3 + 1 a 2
C. 3 - 1 a 2
D. 4 a 2
Người ta thiết kế một bể cá bằng kính không có nắp với thể tích 72
d
m
3
và có chiều cao bằng 3 dm. Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bể dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể. A. a
24...
Đọc tiếp
Người ta thiết kế một bể cá bằng kính không có nắp với thể tích 72 d m 3 và có chiều cao bằng 3 dm. Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bể dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.
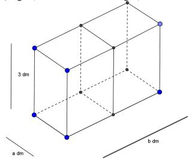
A. a= 24 , b= 21
B. a=3,b=8
C. a=3 2 , b=4 2
D. a=4,b=6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a
a
0
. Hai mặt phẳng (SBC) và
S
C
D
cùng tạo với mặt phẳng (ABCD) một góc
45
°
. Biết
S
B
a
và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tí...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a a > 0 . Hai mặt phẳng (SBC) và S C D cùng tạo với mặt phẳng (ABCD) một góc 45 ° . Biết S B = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
A. 2 a 3 3
B. 2 a 3 6
C. a 3 4
D. 2 a 3 9
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình. A.
1
6
V
B. ...
Đọc tiếp
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên).
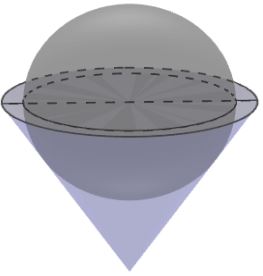
Tính thể tích nước còn lại trong bình.
A. 1 6 V
B. 1 3 V .
C. V
D. 1 π V .
Cho hình chóp đều n cạnh
n
≥
3
. Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng
60
°
, thể tích khối chóp bằng
3
3
4
.
R
3
. Tìm n? A.
n
4...
Đọc tiếp
Cho hình chóp đều n cạnh n ≥ 3 . Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng 60 ° , thể tích khối chóp bằng 3 3 4 . R 3 . Tìm n?
A. n = 4
B. n = 8
C. n = 10
D. n = 6
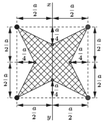
Cho hình vuông ABCD cạnh 4a. Trên cạnh AB và AD lần lượt lấy hai điểm H và K sao cho BH 3HA và AK 3KD. Trên đường thẳng vuông góc tại H lấy điểm S sao cho
S
B
H
^
30
∘
. Gọi E là giao điểm của CH và BK. Tính thể tích của khối cầu ngoại tiếp của hình chóp SAHEK. A.
52...
Đọc tiếp
Cho hình vuông ABCD cạnh 4a. Trên cạnh AB và AD lần lượt lấy hai điểm H và K sao cho BH = 3HA và AK = 3KD. Trên đường thẳng vuông góc tại H lấy điểm S sao cho S B H ^ = 30 ∘ . Gọi E là giao điểm của CH và BK. Tính thể tích của khối cầu ngoại tiếp của hình chóp SAHEK.
A. 52 a 3 13 3
B. 52 a 3 12 3
C. a 3 13 3
D. 54 a 3 13 3
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng
3
a. Thể tích khối chóp S.ABCD bằng A.
a
3
3
3
B.
4
a
3
3
C.
a
3
3
D. ...
Đọc tiếp
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng 3 a. Thể tích khối chóp S.ABCD bằng
A. a 3 3 3
B. 4 a 3 3
C. a 3 3
D. a 3 4 3 3