Đáp án: A.
Vì
nên tích phân đã cho bằng:
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Biết điểm M thuộc đồ thị hàm số y= 3x+4/x-1 và có tung độ bằng 10. Hoành độ điểm M có giá trị bằng:
A. -1
B. 2
C. 4
D. 0
24 tháng 1 2022 lúc 22:03
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho ba vectơ: a→ = (2; -5; 3), b→ = (0; 2; -1), c→ = (1; 7; 2)
Tính tọa độ của vectơ e→ = a→ - 4b→ - 2c→
Câu 24/Đề 1:Cho đồ thị (C):y=x3-3x2+1. Tiếp tuyến của (C) tại điểm có hoành độ bằng 3 tạo với hai trục toạ độ thành một tam giác có diện tích bằng:
A.234
B.117
C.\(\dfrac{238}{9}\)
D.\(\dfrac{338}{9}\)
Cho phương trình az^2+bz+c0 với a,b,c ∈ R , a ≠ 0 có các nghiệm z1,z2 đều không là số thực . Tính P |z1 +z2|2 + |z1 -z2|2 theo a,b,cA: P dfrac{b^2-2ac}{a^2}B: P dfrac{2c}{a}C: Pdfrac{4c}{a}D: P dfrac{2b^2-4ac}{a^2}
Đọc tiếp
Cho phương trình \(az^2+bz+c=0\) với a,b,c ∈ R , a ≠ 0 có các nghiệm z1,z2 đều không là số thực . Tính P |z1 +z2|2 + |z1 -z2|2 theo a,b,c
A: P= \(\dfrac{b^2-2ac}{a^2}\)
B: P= \(\dfrac{2c}{a}\)
C: P=\(\dfrac{4c}{a}\)
D: P= \(\dfrac{2b^2-4ac}{a^2}\)
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
Nếu
a
3
/
3
a
2
/
2
và
log
b
3
/
4
...
Đọc tiếp
Nếu a 3 / 3 > a 2 / 2 và log b 3 / 4 < log b 4 / 5 thì:
A. 0 < a < 1, b > 1 B. 0 < a < 1, 0 < b < 1
C. a > 1, b > 1 D. a > 1, 0 < b < 1
Nếu
a
3
/
3
a
2
/
2
và
log
b
(
3
/
4
)
log
b
(
4
/
5
)
thì:A. 0 a 1, b 1 B. 0 a 1, 0 b 1C....
Đọc tiếp
Nếu a 3 / 3 > a 2 / 2 và log b ( 3 / 4 ) < log b ( 4 / 5 ) thì:
A. 0 < a < 1, b > 1 B. 0 < a < 1, 0 < b < 1
C. a > 1, b > 1 D. a > 1, 0 < b < 1
Cho A(1; -2; 1), B(0; -1; 3),
C
-
2
;
0
;
4
, D(0; 2; -2). Gọi (P) là mp chiếu A, B và (P) cách đều C, D. Biết C, D thuộc 2 phía của (P). Tìm một vectơ pháp tuyến của (P).
Đọc tiếp
Cho A(1; -2; 1), B(0; -1; 3), C - 2 ; 0 ; 4 , D(0; 2; -2). Gọi (P) là mp chiếu A, B và (P) cách đều C, D. Biết C, D thuộc 2 phía của (P). Tìm một vectơ pháp tuyến của (P).
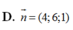
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Tìm góc giữa hai đường thẳng AB và CD