\(4x^2-9=5x+6\sqrt{x+1}\) (ĐK: \(x\ge-1\))
\(\Leftrightarrow4x^2-5x-9=6\sqrt{x+1}\)
\(\Leftrightarrow4x^2+4x-9x-9=6\sqrt{x+1}\)
\(\Leftrightarrow4x\left(x+1\right)-9\left(x+1\right)=6\sqrt{x+1}\)
\(\Leftrightarrow\left(x+1\right)\left(4x-9\right)-6\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}\left[\left(4x-9\right)\sqrt{x+1}-6\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+1}=0\\\left(4x-9\right)\sqrt{x+1}=6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\\left(16x^2-72x+81\right)\left(x+1\right)=36\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\16x^3-56x^2+9x-45=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\\left(x-3\right)\left(4x-5\right)\left(4x+3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=3\left(tm\right)\\x=\dfrac{5}{4}\left(tm\right)\\x=-\dfrac{3}{4}\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{-1;3;\dfrac{5}{4};-\dfrac{3}{4}\right\}\)
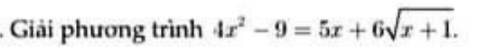
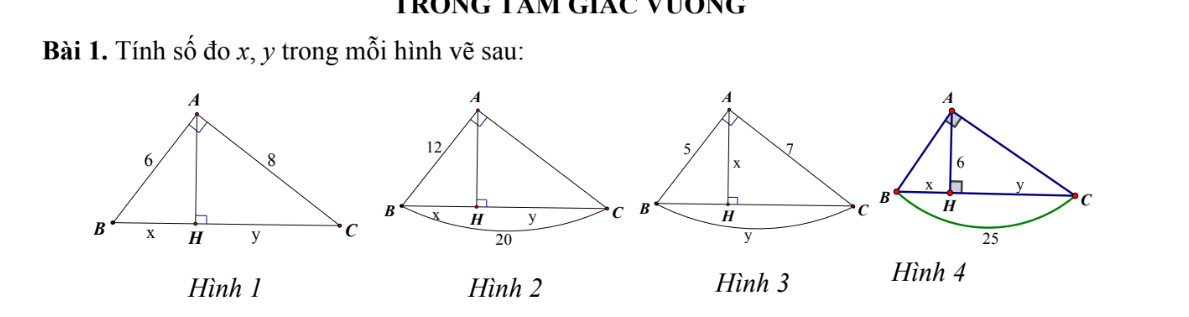bạn nào giúp mình hình 4 với ạ!!
