Bài 9: Xác định hàm số y= ax+b biÕt
a) Đồ thị của hàm số qua A(1;-1) và có hệ số góc là 2
b) Đồ thị của hàm số // với đường thẳng y =-3x + 2 và cắt trục tung tại điểm có tung độ bằng 1.
Bài 10: Cho hàm số: y = -x + 2.
a) Vẽ đồ thị của hàm số trên.
b)Gọi A, B là giao điểm của đồ thị hàm số với các trục tọa độ. Tính khoảng cách từ gốc tọa độ O đến đường thẳng AB.
Bài 10:
a: 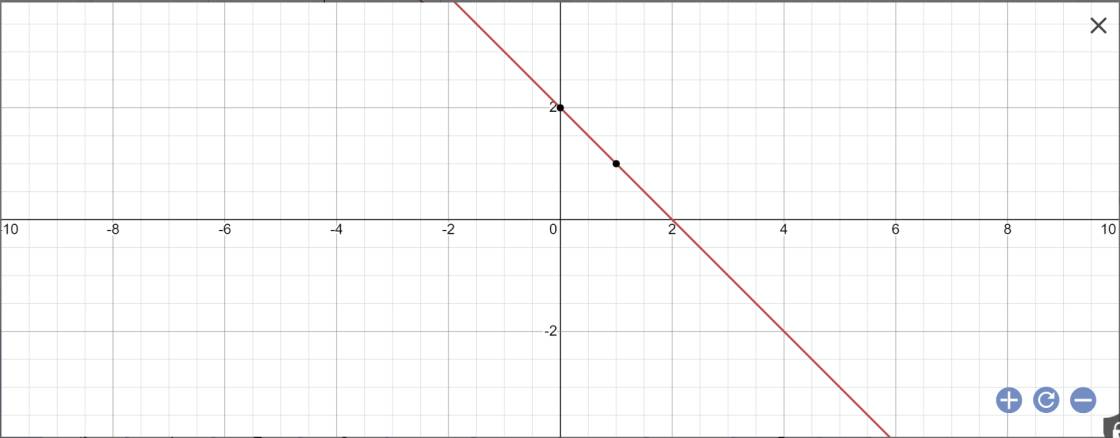
b:
y=-x+2
=>y+x-2=0
=>x+y-2=0
Khoảng cách từ O đến đến đường thẳng AB sẽ bằng khoảng cách từ O đến (d): y=-x+2
=>Khoảng cách từ O đến đường thẳng AB là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot1+0\cdot1+\left(-2\right)\right|}{\sqrt{1^2+1^2}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Bài 9:
a: Vì hệ số góc của hàm số y=ax+b là 2 nên a=2
=>y=2x+b
Thay x=1 và y=-1 vào y=2x+b, ta được:
\(b+2\cdot1=-1\)
=>b+2=-1
=>b=-3
vậy: y=2x-3
b: Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=-3x+2 nên \(\left\{{}\begin{matrix}a=-3\\b\ne2\end{matrix}\right.\)
Vậy: y=-3x+b
Thay x=0 và y=1 vào y=-3x+b, ta được:
\(b-3\cdot0=1\)
=>b-0=1
=>b=1
Vậy: y=-3x+1
Bài 9:
a. Hệ số góc của đths là $2$, tức $a=2$
ĐTHS đi qua điểm $A(1;-1)$ nên:
$-1=a.1+b$
$\Leftrightarrow -1=2.1+b\Rightarrow b=-3$
Vậy hàm số cần tìm là $y=2x-3$
b.
ĐTHS song song với $y=-3x+2$ nên $a=-3$
ĐTHS cần tìm cắt trục tung tại điểm có tung độ $1$, tức là nó đi qua điểm $(0;1)$
$\Rightarrow 1=a.0+b\Rightarrow b=1$
Vậy đths cần tìm là $y=-3x+1$
Bài 10:
a. Bạn chọn 2 điểm bất kỳ thuộc ĐTHS và nối lại sẽ được đồ thị hàm số cần tìm.
b.
$A\in Ox\Rightarrow y_A=0$
Có: $0=y_A=-x_A+2\Rightarrow x_A=2$. Vậy điểm $A$ có tọa độ $(2;0)$
$B\in Oy\Rightarrow x_B=0$
$y_B=-x_B+2=-0+2=2$. Vậy điểm $B$ có tọa độ $(0;2)$
Gọi $d$ là khoảng cách từ $O$ đến $AB$. Theo công thức hệ thức lượng trong tam giác vuông:
$\frac{1}{d^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{|x_A|^2}+\frac{1}{|y_B|^2}$
$=\frac{1}{2^2}+\frac{1}{2^2}=\frac{1}{2}$
$\Rightarrow d=\sqrt{2}$













