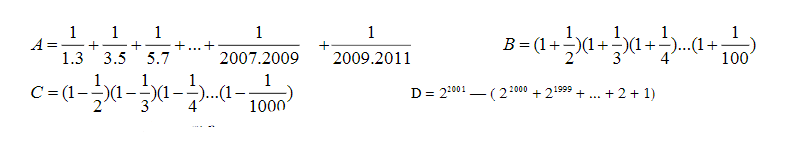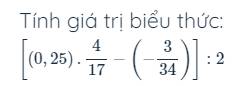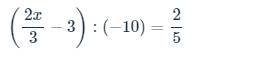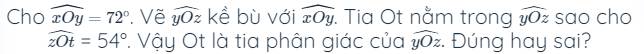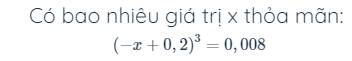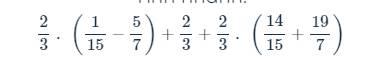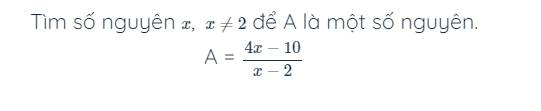a: Ta có: \(A=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2009\cdot2011}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2009\cdot2011}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2010}{2011}=\dfrac{1005}{2011}\)
b: Ta có: \(B=\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)+...+\left(1+\dfrac{1}{100}\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=\dfrac{101}{2}\)
\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2007.2009}+\dfrac{1}{2009.2011}\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2007}-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2011}\right)\)
\(=\dfrac{1005}{2011}\)
\(B=\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)\left(1+\dfrac{1}{4}\right)...\left(1+\dfrac{1}{100}\right)\)
\(=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}...\dfrac{101}{100}\)
\(=\dfrac{101}{2}\)
\(C=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)...\left(1-\dfrac{1}{1000}\right)\)
\(=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{99}{100}\)
\(=\dfrac{1}{100}\)
\(D=2^{2001}-\left(2^{2000}+2^{1999}+...+2+1\right)\)
\(=2^{2001}-2^{2000}-2^{1999}-...-2-1\)
\(=2^{2000}\left(2-1\right)-2^{1999}-...-2-1\)
\(=2^{2000}-2^{1999}-2^{1998}...-2-1\)
\(=2^{1999}\left(2-1\right)-2^{1998}...-2-1\)
\(=2^{1999}-2^{1998}-2^{1997}...-2-1\)
\(=2-1=1\)