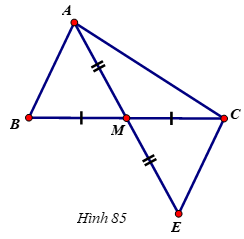
Bài 5 (3,5 điểm) : Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = AM.
a) Chứng minh: Δ ABM = Δ ECM
b) Chứng minh: AB = CE và AB // CE
c) Chứng minh: AC // BE
d) Trên đoạn thẳng AB lấy điểm I, trên đoạn thẳng CE lấy điểm K sao cho AI = EK. Chứng minh: 3 điểm I, M, K thẳng hàng
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Ta có: ΔMAB=ΔMEC
=>AB=EC
Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
c: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
d: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)
nên \(\widehat{KME}+\widehat{IME}=180^0\)
=>I,M,K thẳng hàng