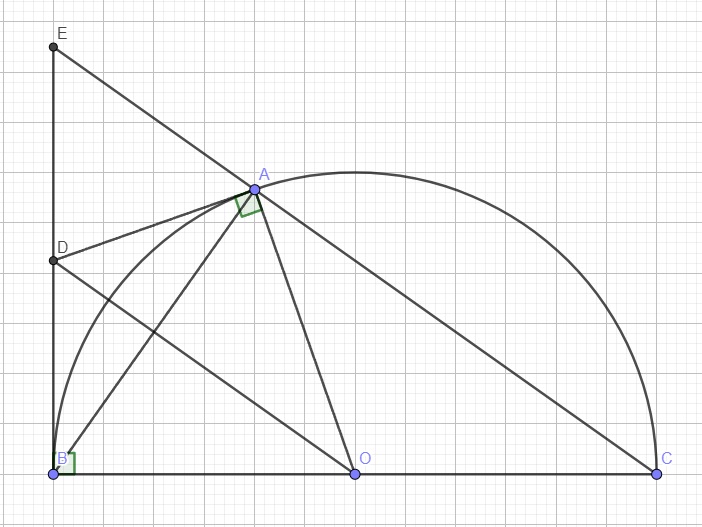
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a.
Do AD là tiếp tuyến tại A \(\Rightarrow\widehat{OAD}=90^0\)
\(\Rightarrow\) 3 điểm O, A, D thuộc đường tròn đường kính OD (1)
BD là tiếp tuyến tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) 3 điểm O, B, D thuộc đường tròn đường kính OD (2)
(1);(2) \(\Rightarrow\) 4 điểm A, D, B, O cùng thuộc đường tròn đường kính OD
b.
Do D là giao điểm 2 tiếp tuyến tại A và B, theo t/c hai tiếp tuyến cắt nhau
\(\Rightarrow DA=DB\)
Mà \(OA=OB=R\)
\(\Rightarrow OD\) là trung trực của AB \(\Rightarrow OD\perp AB\) (3)
BC là đường kính và A thuộc đường tròn nên \(\widehat{BAC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow BA\perp CA\) (4)
(3);(4) \(\Rightarrow OD||CA\) (cùng vuông góc AB) hay \(OD||CE\)
Áp dụng hệ thức lượng trong tam giác vuông BCE với đường cao BA ứng với cạnh huyền:
\(BC^2=CA.CE\Rightarrow\left(2R\right)^2=CA.CE\)
\(\Rightarrow CA.CE=4R^2\)
Em kiểm tra lại đề bài, đoạn này là sao nhỉ: "Tiếp tuyến tại 4 của (O) "