Các câu hỏi tương tự
13 tháng 1 lúc 19:28
giúp mình nhé.cảm ơn rất nhiều !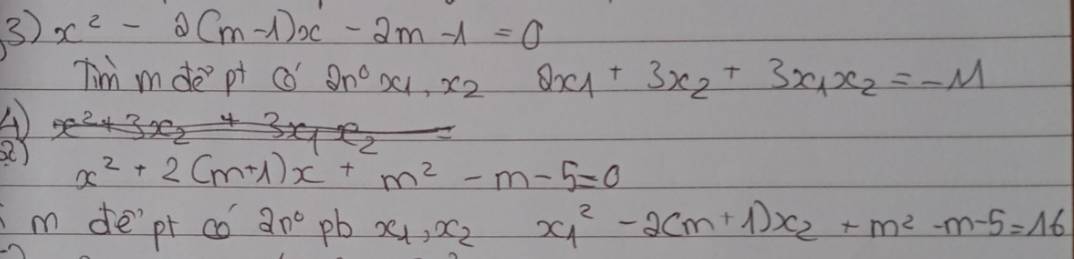
Lưu ý : giải theo cách lớp 9 .bài 3 dùng cách thế 1,2,3; bài 4 dùng cách hạ bậc
22 tháng 10 2021 lúc 22:49
chú ý chỉ làm giùm mk ý b bài 4 thôi nha
Mọi người giúp em bài 3 ý 2 và 3 với 
Giúp mình bài này với (cả 3 ý). Mình cảm ơn nhiều!
Hãy tìm kiếm hoặc nghĩ ra 1 dạng bài tập bao gồm 4 ý:
1 ý co sử dụng tính chất của tiếp tuyến
1 ý co sử dụng hệ thức lượng
1 ý có sử dung đến tính toán
1 ý dùng bất đẳng thức hinh học hoặc có yếu tố chuyển động
Thầy cô giúp em bài 2 ý 1 và 3 với ạ, em đang cần gấp ạ 
Mình muốn giao lưu với các bạn học toán qua bài chứng minh bất đẳng thức sau :v Trước khi trình bày bài toán các bạn nêu ý tưởng nhéChứng minh với mọi a+b+c0 ta cófrac{a^3+b^3+c^3}{3}.frac{a^4+b^4+c^4}{4}frac{a^7+b^7+c^7}{7}2.Giải hệ phương trình hept{begin{cases}x^2+y^2+x+yleft(x+1right)left(y+1right)left(frac{x}{y+1}right)^2+left(frac{y}{x+1}right)^21end{cases}}
Đọc tiếp
Mình muốn giao lưu với các bạn học toán qua bài chứng minh bất đẳng thức sau :v Trước khi trình bày bài toán các bạn nêu ý tưởng nhé
Chứng minh với mọi a+b+c=0 ta có
\(\frac{a^3+b^3+c^3}{3}.\frac{a^4+b^4+c^4}{4}=\frac{a^7+b^7+c^7}{7}\)
2.Giải hệ phương trình
\(\hept{\begin{cases}x^2+y^2+x+y=\left(x+1\right)\left(y+1\right)\\\left(\frac{x}{y+1}\right)^2+\left(\frac{y}{x+1}\right)^2=1\end{cases}}\)
e nhờ thầy cô và các bạn gợi ý giúp em bài 4 với ạ
giúp mk bài này nhé
so sánh căn 3 và 5- căn 8
*lưu ý: k dùng máy tính
Tình cờ kiếm trên AoPS được bài này hơi hay đấy!:)) Ý tưởng của họ tuyệt vời quá, em chả hiểu nổi làm sao có đc ý tưởng như vậy:V Để xem mọi người có ý tưởng thế nào:))
Cho a, b là các số dương thỏa mãn \(ab\ge\frac{3}{2}\)
Chứng minh rằng: \(3\left(2a+b-3\right)\left(2b+a-3\right)\ge\left(a-b\right)^2+\frac{21}{20}\)