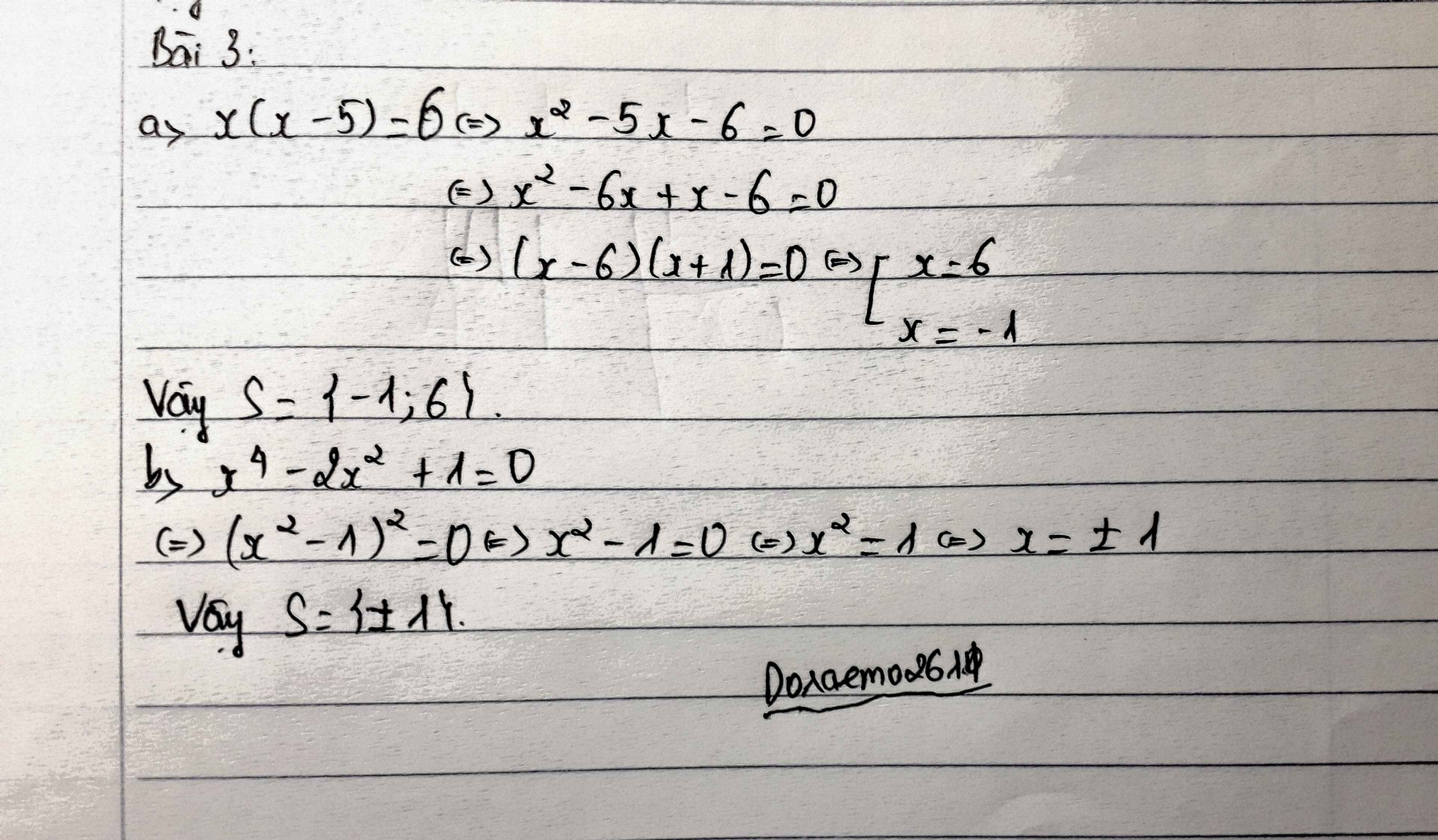Question

Bài 3: Giải phương trình :

a) x ( x - 5 ) = 6

b) x⁴ - 2x² +1 = 0

Answer 1

a) \(x^2-5x-6=0\)

⇔\(\left(x^2+x\right)-\left(6x+6\right)=0\)

\(\Leftrightarrow\left(x-6\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-1\end{matrix}\right.\)

b) \(x^4-2x^2+1=0\)

\(\Leftrightarrow\left(x^2-1\right)^2=0\)

\(\Leftrightarrow x^2=1\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

Answer 2

a) x ( x - 5 ) = 6

<=> x^2-5x-6=0

Ta thấy : 1-(-5)-6=0

=> x₁=-1; x₂=6

b) x⁴ - 2x² +1 = 0

Đặt t=x² với t\(\ge0\)

Ta có: t²-2t+1=0

<=>(t-1)²=0

<=> t=1

<=> x₁=1;x₂=-1

Answer 3