Question

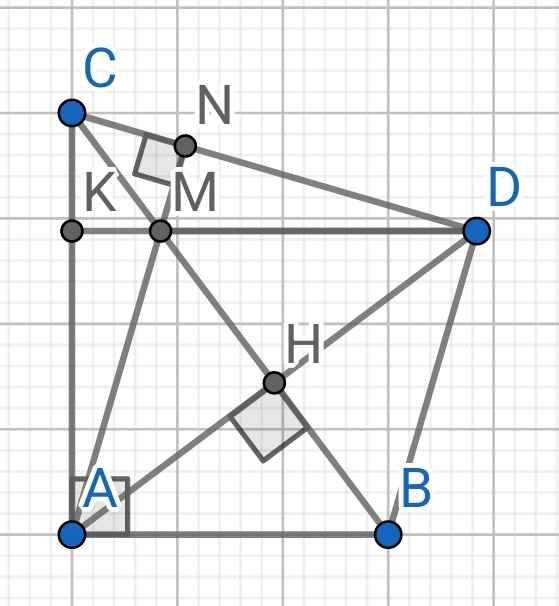
Bài 2: Cho tam giác ABC vuông tại A (AB<AC). Vẽ AH vuông góc với BC (H thuộc BC). Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA.

a, C/m rằng tam giác ABH = tam giác BDH và tia BC là tia phân giác của góc ABD.

b, Qua D vẽ đường thẳng song song với AB, Cắt BC tại M và cắt AC tại K. C/m rằng AD là đường trung trực của đoạn thẳng BM.

C, Vẽ đường thẳng CN vuông góc với đường thẳng AM (N thuộc AM). C/m 3 điểm C, N, D thẳng hàng.

Answer 1

 a) Sửa đề: Chứng minh ABH = DBH

Giải:

Xét hai tam giác vuông: ∆ABH và ∆DBH có:

BH là cạnh chung

AH = DH (gt)

⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)

⇒ ∠ABH = ∠DBH (hai góc tương ứng)

⇒ BH là tia phân giác của ∠ABD

b) Do DM // AB (gt)

⇒ ∠MDH = ∠HAB (so le trong) (1)

Do ∆ABH = ∆DBH (cmt)

⇒ ∠HAB = ∠HDB (hai góc tương ứng) (2)

Từ (1) và (2) ⇒ ∠MDH = ∠HDB

Xét hai tam giác vuông: ∆DHM và ∆DHB có:

DH là cạnh chung

∠MDH = ∠HDB (cmt)

⇒ ∆DHM = ∆DHB (cạnh góc vuông - góc nhọn kề)

⇒ ∠DHM = ∠DHB (hai góc tương ứng)

Mà ∠DHM + ∠DHB = 180⁰ (kề bù)

⇒ ∠DHM = ∠DHB = 180⁰ : 2 = 90⁰

⇒ DH ⊥ BM (3)

Do ∆DHM = ∆DHB (cmt)

⇒ HM = HB

⇒ H là trung điểm của BM (4)

Từ (3) và (4) ⇒ HD là đường trung trực của BM

⇒ AD là đường trung trực của BM

c) Do AD là đường trung trực của BM (cmt)

⇒ AD ⊥ CH

Do DK // AB (gt)

⇒ DK ⊥ AC (AB ⊥ AC)

∆ACD có:

CH là đường cao (CH ⊥ AD)

DK là đường cao thứ hai (DK ⊥ AC)

⇒ AM là đường cao thứ ba

Mà AM ⊥ CN tại N

⇒ AN là đường cao thứ ba của ∆ACD

⇒ C, N, D thẳng hàng