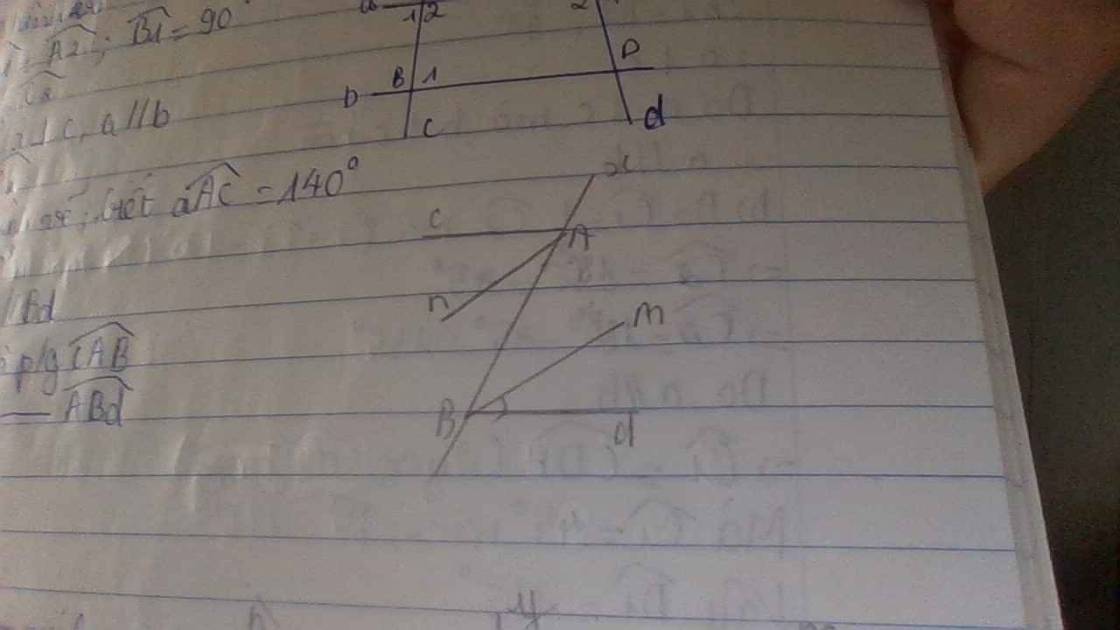Question

bài 2: cho hình vẽ, biết góc aAc = 140 độ, góc ABd= 40 độ

a) c/m Ac//Bd

b) gọi Am là p/g góc cAB

Gọi Bm là p/g góc ABd

c) c/m An//Bm

Giúp mình với ạ, chiều nay mình học rùi

Answer 1

a) Để chứng minh rằng Ac//Bd, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn đều bằng 180 độ. Vì góc aAc = 140 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 140 độ + 40 độ = 180 độ. Do đó, ta có Ac//Bd.

b) Để chứng minh rằng Am là phân giác góc cABG, ta cần chứng minh rằng góc cAmB = góc cABG. Vì góc cAmB là góc nội tiếp trên cung cùng phía với góc cABG, nên góc cAmB = (180 độ - góc cABG) / 2 = (180 độ - 140 độ) / 2 = 40 độ. Vậy, Am là phân giác góc cABG.

c) Để chứng minh rằng An//Bm, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn là 180 độ. Vì góc cAmB = 40 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 40 độ + 40 độ = 80 độ. Do đó, ta không thể kết luận rằng An//Bm.

Answer 2

khó quaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaas

Answer 3

a: góc cAa=góc dBA

mà hai góc này là hai góc so le trong

nên Ac//Bd

b: góc cAn=góc BAn=140/2=70 độ

Bm là phân giác của góc dBA
=>góc dBm=góc ABm=140/2=70 độ

góc nAB=góc mBA

mà hai góc so le trong

nên An//Bm