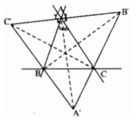
a: Các đường cao của ΔHBC là BF,HD,CE
Vì BF,HD,CE đồng quy tại H
nên H là trực tâm của ΔHBC
b: Xét ΔHAB có
HF\(\perp\)AB
AE\(\perp\)BH tại E
BD\(\perp\)AH tại D
HF,AE,BD đồng quy tại H
Do đó: H là trực tâm của ΔHAB
Xét ΔHAC có
HE\(\perp\)AC tại E
CD\(\perp\)AH tại D
AF\(\perp\)HC tại F
HE,CD,AF đồng quy tại H
Do đó: H là trực tâm của ΔHAC
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự hãy chỉ ra trực tâm của các tam giác HAB và HAC.
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự hãy chỉ ra trực tâm của các tam giác HAB và HAC.
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB, HAC
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
Cho tam giác ABC không vuông.Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC.Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
cho tam giác abc nhọn vẽ các đg cao AM,BN,CE cắt nhau tại H.Hãy chỉ ra trực tâm của mỗi tam giác có trên hình
Cho tam giác ABC, Hai đường phân giác của các cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cắt nhau tại A', B', C'. Chứng minh rằng AA', BB', CC' là các đường cao của tam giác A'B'C'. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.
Bài 4. Tam giác ABC cân tại A có góc A = 120°, các đường trung trực của AB và AC cắt nhau tại O, căt cạnh BC lần lượt tại E và F Chứng minh E là trực tâm, trọng tâm tam giác OAB và F là trực tâm, trọng tâm tam giác OAC Bài 5. Tam giác ABC. Qua các đinh A, B, C kẻ các đường thắng song song với cạnh đôi diện, chúng cắt nhau tạo thành tam giác DEF. Chứng minh răng các đường cao của tam giác ABC là các đường trung trực của tam giác DEF MECA và lấy điểm N sao c
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
Các bạn giải giúp mình bài này nha
Cho tam giac ABC. Hai đường phân giác của cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cách nhau tại A', B', C'. Chứng minh rằng AA', BB',CC' là các đường cao cua tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'
(Các bạn vẽ hình dùm mình luôn nha)
