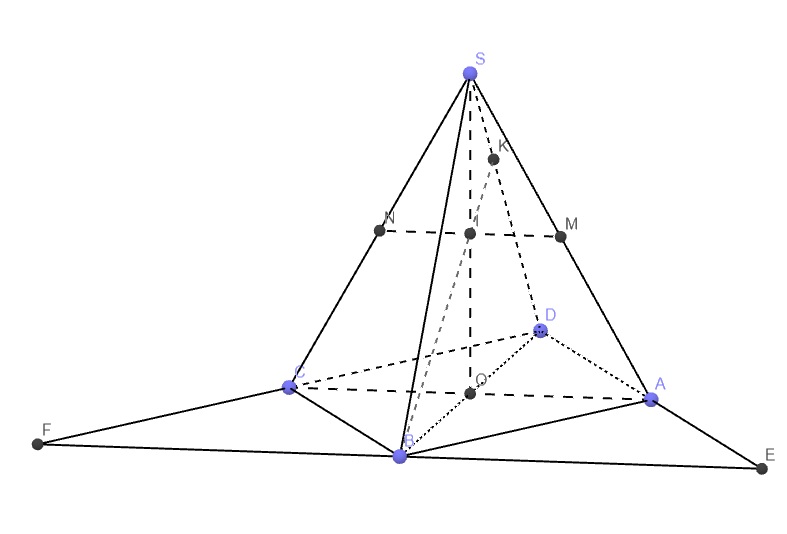
Bài 11: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC.
a) Tìm giao tuyến của (BMN) và (ABCD).
b) Gọi \(K=SD\cap\left(BMN\right)\). Tính tỉ số \(\dfrac{SK}{SD}\).
c) Tìm \(E=AD\cap\left(MNB\right)\) và \(F=CD\cap\left(MNB\right)\). Chứng minh B, E, F thẳng hàng.
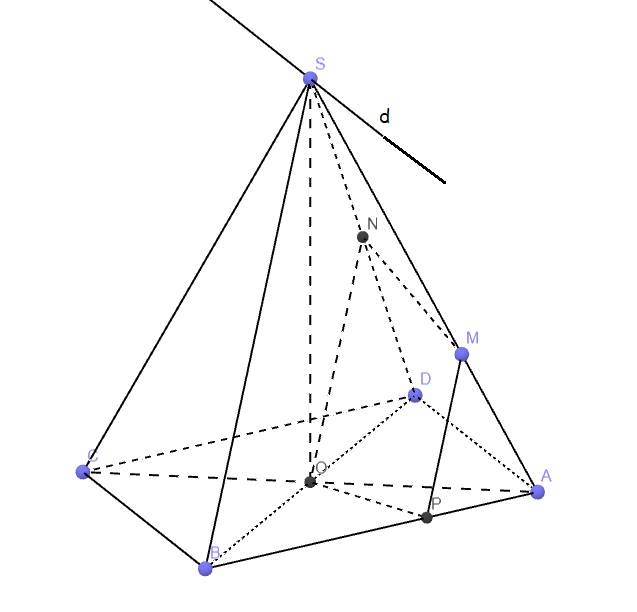
Bài 12: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là các điểm lần lượt thuộc các cạnh SA, SD sao cho \(\dfrac{SM}{SA}=\dfrac{2}{3}\) và \(\dfrac{SN}{SD}=\dfrac{1}{2}\).
a) Chứng minh rằng ON//SB.
b) Tìm giao tuyến của hai mặt phẳng (SBC) và (SAD).
c) Tìm giao điểm P của AB và mặt phẳng (OMN). Tính tỉ số \(\dfrac{AP}{PB}\).
Bài 13: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3EC. Mặt phẳng (MNE) cắt BD tại F. Tính tỉ số \(\dfrac{FD}{FB}\).
11.
a.
Theo giả thiết suy ra MN là đường trung bình tam giác (SAC)
\(\Rightarrow MN||AC\)
Trong mp (ABCD), qua B kẻ đường thẳng d song song AC
\(\Rightarrow d||MN\) \(\Rightarrow d\in\left(BMN\right)\)
\(\Rightarrow d=\left(BMN\right)\cap\left(ABCD\right)\)
b.
Gọi O là tâm đáy, I là giao điểm của SO và MN
\(\Rightarrow I\) là trung điểm SO theo t/c đường trung bình
Trong mp (SBD), nối BI kéo dài cắt SD tại K
\(\Rightarrow K=SD\cap\left(BMN\right)\)
Áp dụng định lý Menelaus cho tam giác SDO:
\(\dfrac{SK}{KD}.\dfrac{DB}{BO}.\dfrac{OI}{IS}=1\Leftrightarrow\dfrac{SK}{KD}.2.1=1\)
\(\Rightarrow2SK=DK=SD-SK\)
\(\Rightarrow3SK=SD\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}\)
c.
Trong mp (ABCD), gọi E là giao điểm của d và AD
\(\Rightarrow E=AD\cap\left(BMN\right)\)
Gọi F là giao điểm của d và CD
\(\Rightarrow F=CD\cap\left(BMN\right)\)
Hiển nhiên B, E, F đều thuộc d nên thẳng hàng
12.
a.
\(\dfrac{SN}{SD}=\dfrac{1}{2}\Rightarrow N\) là trung điểm SD
O là trung điểm BD (t/c hình bình hành), N là trung điểm SD
\(\Rightarrow ON\) là đường trung bình tam giác SBD
\(\Rightarrow ON||SB\)
b.
Qua S kẻ đường thẳng d song song AD \(\Rightarrow d||BC\)
Do \(\left\{{}\begin{matrix}S\in d\\d||AD\end{matrix}\right.\) \(\Rightarrow d\in\left(SAD\right)\)
\(\left\{{}\begin{matrix}S\in d\\d||BC\end{matrix}\right.\) \(\Rightarrow d\in\left(SBC\right)\)
\(\Rightarrow d=\left(SAC\right)\cap\left(SBD\right)\)
c.
\(\left\{{}\begin{matrix}M\in SA\in\left(SAB\right)\\P\in AB\in\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow MP\in\left(SAB\right)\)
\(P=AB\cap\left(OMN\right)\Rightarrow P\in\left(OMN\right)\Rightarrow MP\in\left(OMN\right)\)
\(\Rightarrow MP=\left(OMN\right)\cap\left(SAB\right)\)
Ba mặt phẳng (OMN), (SBD), (SAB) cắt nhau theo 3 giao tuyến ON, SB, MP nên 3 giao tuyến này song song hoặc đồng quy.
Mà ON song song SB (theo cm câu a)
\(\Rightarrow ON||SB||MP\)
Do đó, qua M kẻ đường thẳng song song SB sẽ cắt AB tại P
\(\dfrac{SM}{SA}=\dfrac{2}{3}\Rightarrow3SM=2SA=2\left(SM+AM\right)\Rightarrow SM=2AM\)
Theo định lý Thales:
\(\dfrac{AP}{BP}=\dfrac{AM}{SM}=\dfrac{1}{2}\)
13.
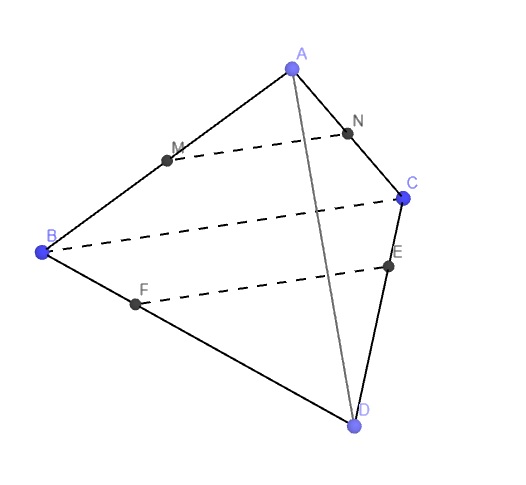
Từ giả thiết suy ra MN là đường trung bình tam giác ABC
\(\Rightarrow MN||BC\)
Trong mp (BCD), qua E kẻ đường thẳng d song song BC
\(\Rightarrow d||MN\Rightarrow d\in\left(EMN\right)\)
Gọi F là giao điểm của d và BD \(\Rightarrow\left\{{}\begin{matrix}F\in BD\\F\in d\in\left(MNE\right)\end{matrix}\right.\)
\(\Rightarrow F=BD\cap\left(MNE\right)\)
Theo định lý Thales:
\(\dfrac{FD}{FB}=\dfrac{ED}{EC}=3\)