Bài 2:
a: xy=z; yz=4x; xz=9y
Do đó: \(xy\cdot yz\cdot xz=z\cdot4x\cdot9y=36xyz\)
=>\(\left(xyz\right)^2=36xyz\)
=>xyz(xyz-36)=0
TH1: xyz=0
=>x=y=z=0
TH2: xyz-36=0
=>xyz=36
Ta có: xyz=36
=>\(z\cdot z=36\)
=>\(z^2=36\)
=>\(\left[\begin{array}{l}z=6\\ z=-6\end{array}\right.\)
Ta có: xyz=36
=>\(4x\cdot x=36\)
=>\(4x^2=36\)
=>\(x^2=9\)
=>\(\left[\begin{array}{l}x=3\\ x=-3\end{array}\right.\)
Ta có: xyz=36
=>\(9y\cdot y=36\)
=>\(9y^2=36\)
=>\(y^2=4\)
=>\(\left[\begin{array}{l}y=2\\ y=-2\end{array}\right.\)
vậy: (x;y;z)∈{(0;0;0);(3;2;6);(-3;-2;-6)}
b: \(3\left(x-2022\right)^2=21-y^2\)
=>\(21-y^2\) ⋮3
=>\(y^2\) ⋮3
=>y⋮3(1)
Ta có: \(3\left(x-2022\right)^2>=0\forall x\)
=>\(21-y^2\ge0\)
=>\(y^2\le21\)
mà y⋮3
và y nguyên
nên y∈{0;3;-3}
TH1: y=0
\(3\left(x-2022\right)^2=21-y^2\)
=>\(3\left(x-2022\right)^2=21\)
=>\(\left(x-2022\right)^2=7\)
=>\(\left[\begin{array}{l}x-2022=\sqrt7\\ x-2022=-\sqrt7\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\sqrt7+2022\left(loại\right)\\ x=-\sqrt7+2022\left(loại\right)\end{array}\right.\)
TH2: y∈{3;-3}
=>\(y^2=9\)
=>\(3\left(x-2022\right)^2=21-9=12\)
=>\(\left(x-2022\right)^2=4\)
=>\(\left[\begin{array}{l}x-2022=2\\ x-2022=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2024\\ x=2020\end{array}\right.\)
vậy: (x;y)∈{(2020;3);(2020;-3);(2024;3);(2024;-3)}
Bài 1:
a: \(\frac{2a-b}{a-b}=\frac23\)
=>3(2a-b)=2(a-b)
=>6a-3b=2a-2b
=>6a-2a=-2b+3b
=>4a=b
=>\(a=\frac{b}{4}\)
\(M=\frac{4ab+2b^2}{8a^2-ab}\)
\(=\frac{b\cdot b+2b^2}{8\cdot\left(\frac{b}{4}\right)^2-b\cdot\frac{b}{4}}\)
\(=\frac{3b^2}{8\cdot\frac{b^2}{16}-\frac{b^2}{4}}=\frac{3b^2}{\frac12b^2-\frac14b^2}=\frac{3b^2}{\frac14b^2}=3:\frac14=12\)
b: ta có công thức tổng quát:
\(1-\frac{1}{1+2+\cdots+n}\)
\(=1-\frac{1}{\frac{n\left(n+1\right)}{2}}=1-\frac{2}{n\left(n+1\right)}\)
\(=\frac{n\left(n+1\right)-2}{n\left(n+1\right)}=\frac{n^2+n-2}{n\left(n+1\right)}=\frac{\left(n+2\right)\left(n-1\right)}{n\left(n+1\right)}\)
Do đó,ta có:
\(1-\frac{1}{1+2}=\frac{\left(2+2\right)\left(2-1\right)}{2\cdot\left(2+1\right)}=\frac{4\cdot1}{2\cdot3}\)
\(1-\frac{1}{1+2+3}=\frac{\left(3+2\right)\left(3-1\right)}{3\left(3+1\right)}=\frac{5\cdot2}{3\cdot4}\)
....
\(1-\frac{1}{1+2+3+\cdots+2024}=\frac{\left(2024+2\right)\left(2024-1\right)}{2024\left(2024+1\right)}=\frac{2026\cdot2023}{2024\cdot2025}\)
Do đó: \(A=\frac{4\cdot1}{2\cdot3}\cdot\frac{5\cdot2}{3\cdot4}\cdot\ldots\cdot\frac{2026\cdot2023}{2024\cdot2025}\)
\(=\frac{1\cdot2\cdot\ldots\cdot2023}{2\cdot3\cdot\ldots\cdot2024}\cdot\frac{4\cdot5\cdot\ldots\cdot2026}{3\cdot4\cdot\ldots\cdot2025}=\frac{1}{2024}\cdot\frac{2026}{3}=\frac{1013}{3\cdot1012}=\frac{1013}{3036}\)

 Mn giúp với cần gấp !!!
Mn giúp với cần gấp !!!





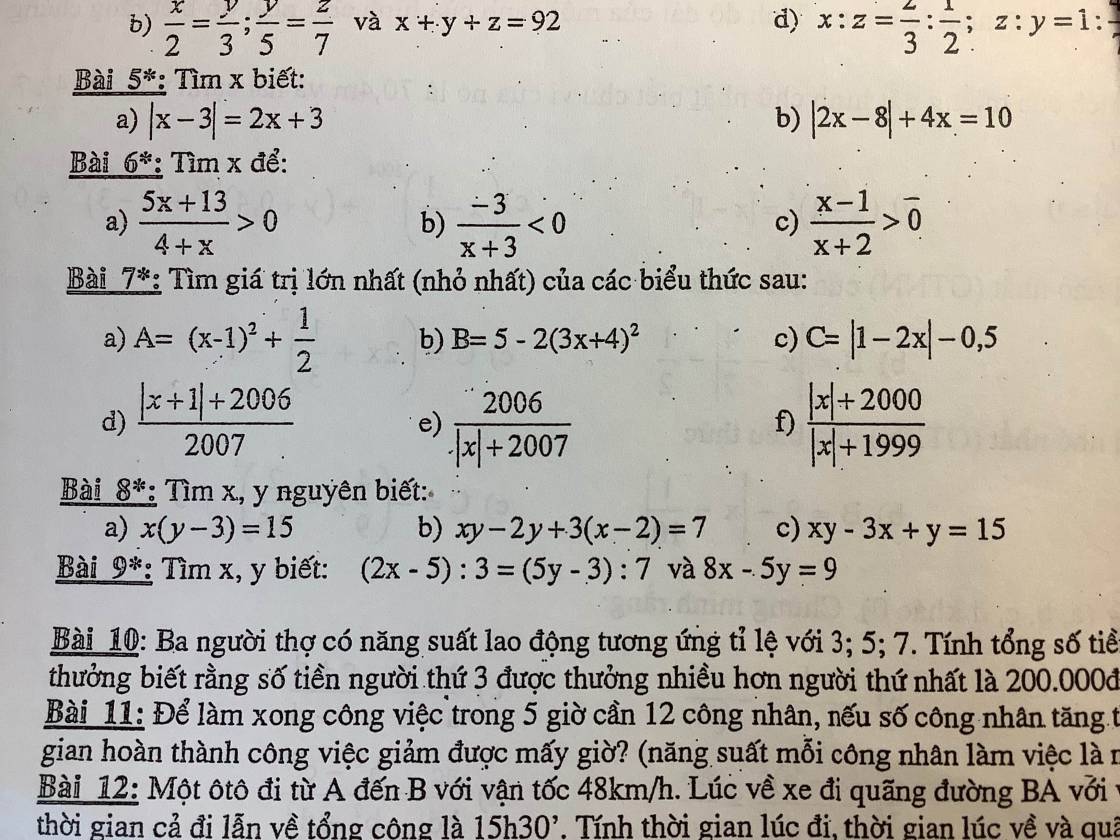

 mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều
mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều
 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!








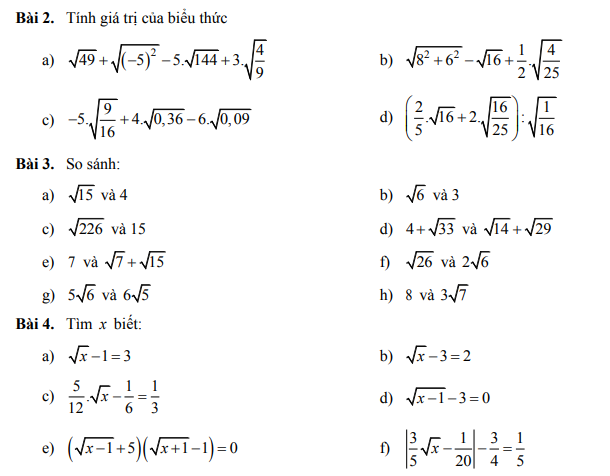 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy