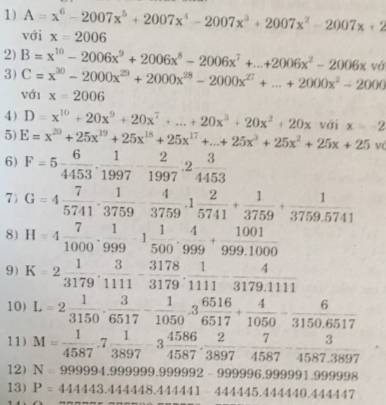1: x=2006 nên x+1=2007
\(A=x^6-x^5\left(x+1\right)+x^4\left(x+1\right)-...-x\left(x+1\right)+2\)
\(=x^6-x^6+x^5+x^5+....-x^2-x+2\)
=2-x
=-2004
6: Đặt 4453=a; 1997=b
Theo đề, ta có:
\(F=\left(5+\dfrac{6}{a}\right)\cdot\dfrac{1}{b}-\dfrac{2}{b}\cdot\left(2+\dfrac{3}{a}\right)\)
\(=\dfrac{5a+6}{a}\cdot\dfrac{1}{b}-\dfrac{2}{b}\cdot\dfrac{2a+3}{a}\)
\(=\dfrac{5a+6-4a-6}{ab}=\dfrac{a}{ab}=\dfrac{1}{b}=\dfrac{1}{1997}\)
Đúng 2
Bình luận (0)
