Ba người chỉ có một chiếc xe đạp cần đi từ A đến B cách nhau là s = 20 km trong thời
gian ngắn nhất. Xe đạp chỉ đi được hai người nên một người phải đi bộ. Đầu tiên người thứ
nhất đèo người thứ hai còn người thứ ba đi bộ, đến một vị trí thích hợp C thì người thứ nhất
để người thứ hai đi bộ tiếp đến B còn mình quay xe lại để đón người thứ ba. Cả ba người
đến B đồng thời. Tốc độ đi bộ là v1 = 4km/h, tốc độ xe đạp là v2 = 20km/h.
a) Xác định vị trí C nơi người thứ nhất thả người thứ hai xuống đi bộ.
b) Tính thời gian chuyển động từ lúc xuất phát đi từ A đến lúc ba người đến B.
Chia đoạn đường làm 3 phần như sau.
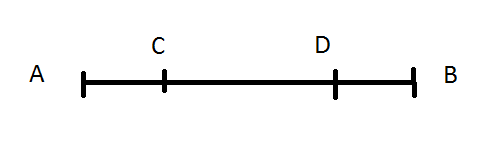
a)Coi C là nơi người thứ nhất thả người thứ 2 đi bộ.
Coi D là nơi người thứ nhất và ba gặp nhau.
\(CD=AB-\left(AC+BD\right)=AB-2BD\)
Thời gian xe thứ hai đi là:
\(t_2=\dfrac{AD}{v_2}+\dfrac{BD}{v_1}=\dfrac{20-BD}{v_2}+\dfrac{BD}{v_1}\)
Thời gian xe thứ nhất đi:
\(t_1=\dfrac{AD+BD+2CD}{v_2}=\dfrac{AB+2CD}{v_2}=\dfrac{3AB-4BD}{v_2}\)
Theo bài: \(t_1=t_2\Rightarrow\dfrac{20-BD}{v_2}+\dfrac{BD}{v_1}=\dfrac{3AB-4BD}{v_2}\)
\(\Rightarrow\dfrac{20-BD}{20}+\dfrac{BD}{4}=\dfrac{3\cdot20-4BD}{20}\Rightarrow BD=5km\)
Vị trí C cần tìm là:
\(CD=AB-2BD=20-2\cdot5=10km\)
b)Thời gian chuyển động từ lúc xuất phát đi từ A đến lúc ba người đến B là:
\(t_2=\dfrac{20-BD}{v_2}+\dfrac{BD}{v_1}=\dfrac{20-5}{20}+\dfrac{5}{4}=2h\)














