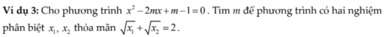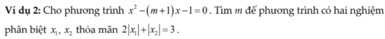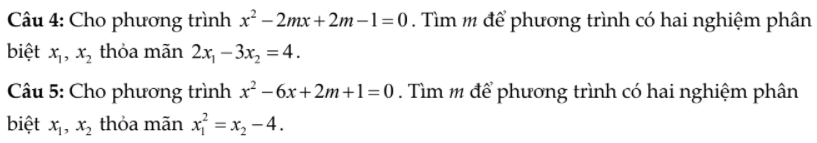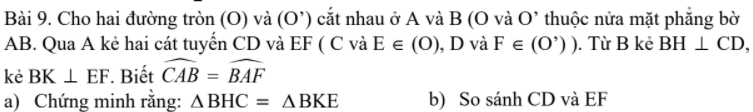\(\Delta'=m^2-\left(m-1\right)=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy pt luôn có 2 nghiệm pb
Ta có : \(x_1+x_2+2\sqrt{x_1x_2}=4\Leftrightarrow2m+2\sqrt{m-1}=4\)
\(\Leftrightarrow\sqrt{m-1}=2-m\)
đk : m =< 2
TH1 \(m-1=2-m\Leftrightarrow m=\dfrac{3}{2}\)(tm)
TH2 \(m-1=m-2\)( vô lí )
\(\Delta'=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m-1\end{matrix}\right.\)
Để biểu thức \(\sqrt{x_1}+\sqrt{x_2}=2\) xác định \(\Rightarrow x_1;x_2\ge0\Rightarrow\left\{{}\begin{matrix}x_1+x_2\ge0\\x_1x_2\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2m\ge0\\m-1\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
Khi đó:
\(\sqrt{x_1}+\sqrt{x_2}=2\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4\)
\(\Leftrightarrow2m+2\sqrt{m-1}=4\)
\(\Leftrightarrow m+\sqrt{m-1}=2\)
Đặt \(\sqrt{m-1}=t\ge0\Rightarrow m=t^2+1\)
\(\Rightarrow t^2+1+t=2\Rightarrow t^2+t-1=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-1+\sqrt{5}}{2}\\t=\dfrac{-1-\sqrt{5}}{2}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{m-1}=\dfrac{-1+\sqrt{5}}{2}\Rightarrow m-1=\dfrac{3-\sqrt{5}}{2}\)
\(\Rightarrow m=\dfrac{5-\sqrt{5}}{2}\)