\(a,\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2-4m+3\right)\\ =m^2+2m+1-m^2+4m-3\\ =6m-2\)
Để pt vô nghiệm thì \(6m-2< 0\Leftrightarrow m< \dfrac{1}{3}\)
Để pt có nghiệm kép thì \(6m-2=0\Leftrightarrow m=\dfrac{1}{3}\)
Để pt có 2 nghiệm phân biệt thì \(6m-2>0\Leftrightarrow m>\dfrac{1}{3}\)
\(b,\Delta=\left(m-3\right)^2-4.\left(-3m\right)\\ =m^2-6m+9+12m\\ =m^2+6m+9\\ =\left(m+3\right)^2\ge0\)
Suy ra pt luôn không vô nghiệm với mọi m
PT có nghiệm kép khi \(\left(m+3\right)^2=0\Leftrightarrow m=-3\)
PT có 2 nghiệm phân biệt khi \(\left(m+3\right)^2>0\Leftrightarrow m\ne-3\)








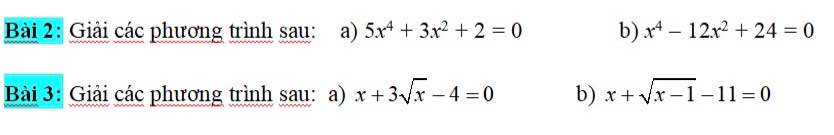




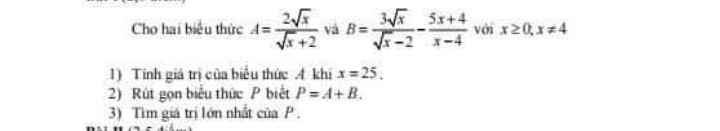

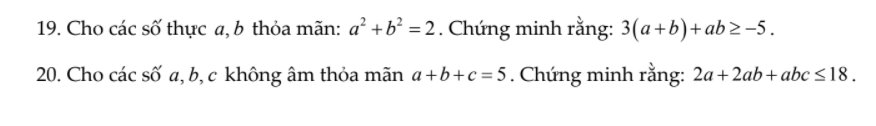






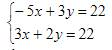 ai giúp em bài này với ạ 🥺 :)
ai giúp em bài này với ạ 🥺 :)