1: \(AB=\dfrac{1}{2}CD\)
\(CE=ED=\dfrac{CD}{2}\)
Do đó: AB=CE=ED
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
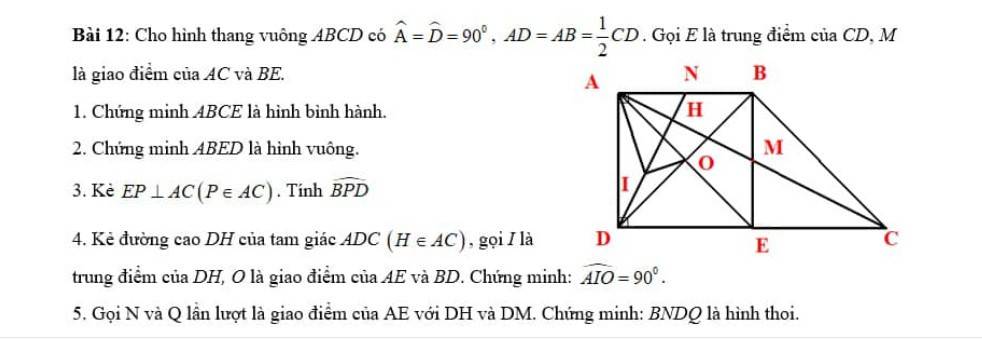
2: Xét tứ giác ABED có
AB//ED
AB=ED
Do đó: ABED là hình bình hành
Hình bình hành ABED có AB=AD
nên ABED là hình thoi
Hình thoi ABED có \(\widehat{BAD}=90^0\)
nên ABED là hình vuông
3: Gọi giao điểm của AE và BD là L
ABED là hình vuông
=>AE=BD và AE vuông góc với BD tại trung điểm của mỗi đường
=>L là trung điểm chung của AE và BD và AE=BD
=>\(LA=LE=LB=LD=\dfrac{BD}{2}=\dfrac{AE}{2}\)
ΔAPE vuông tại P
mà PL là đường trung tuyến
nên \(PL=\dfrac{AE}{2}=\dfrac{BD}{2}\)
Xét ΔBPD có
PL là đường trung tuyến
\(PL=\dfrac{BD}{2}\)
Do đó: ΔBPD vuông tại P
=>\(\widehat{BPD}=90^0\)








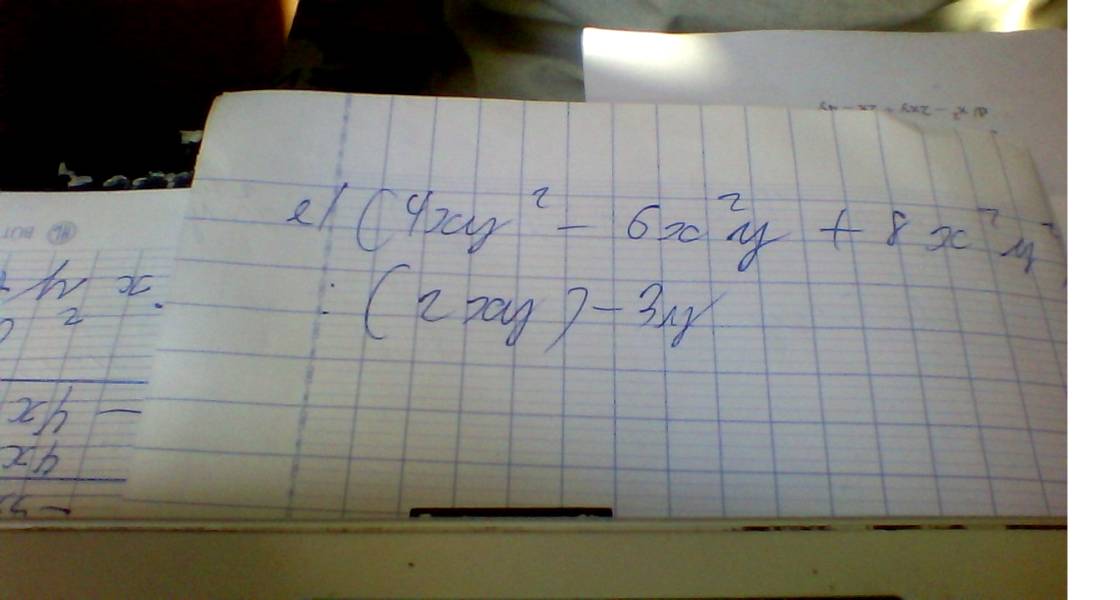


 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn